Airy Disk와 Diffraction Limit(회절 한계)

본 내용은 이미징 리소스 가이드의 단원 2.4에 해당합니다.

Airy Disk

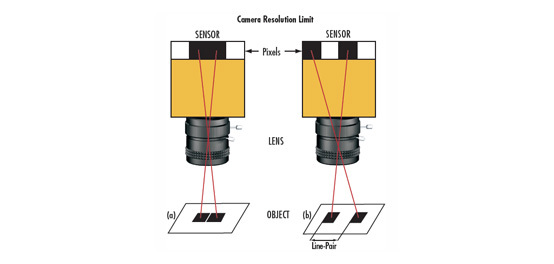
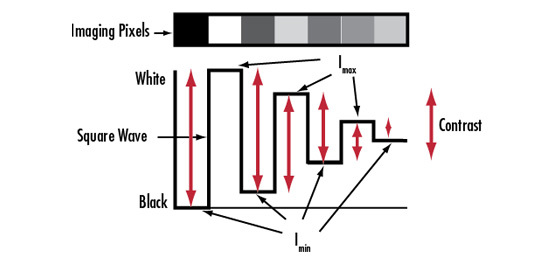
모든 렌즈는 finite aperture가 있는데 빛이 임의의 크기를 가진 조리개(aperture)를 통과하면 회절이 발생합니다. 그 결과 중심부는 밝고 주변부는 강도가 점차 감소하는 일련의 동심원 링으로 이루어진 회절 패턴이 생성되며 이를 소위 Airy disk라고 합니다(그림 1 참조). Airy disk는 광선이 초점을 맺을 수 있는 가장 작은 지점이 있기 때문에 이 패턴의 직경은 조명 빛의 파장(λ)과 원형 구경의 크기와 관련되어 있다는 점을 명심해야 합니다. 피사체의 서로 다른 디테일에 초점을 맞춘 Airy 패턴은 서로 근접해가면서 중첩되기 시작합니다(Contrast(콘트라스트) 편 참조). 중첩된 패턴이 콘트라스트를 감소시키기에 충분한 보강 간섭을 일으키면 결국 이 패턴들은 서로 구분할 수 없게 됩니다. 그림 1은 f/2.8로 설정된 렌즈와 f/8로 설정된 렌즈에서 스폿 크기의 차이를 보여줍니다. 픽셀 크기가 계속해서 줄어들수록 이는 더 큰 문제로 이어지게 됩니다. Airy disk $ \left( \varnothing_{\small{\text{Airy Disk}}} \right) $ 혹은 최소 스폿 크기는 f/#와 파장(λ)을 사용하여 계산할 수 있습니다.

(1)$$ \varnothing _{\small{\text{Airy Disk}}} \approx 2.44 \times \lambda \times \left( \text{f} / \# \right) $$

(1)

$$ Ø_{\small{\text{Airy Disk}}} \approx 2.44 \times \lambda \times \left( \text{f} / \# \right) $$

그림 1: 이미징 렌즈의 조리개가 닫히면 회절이 증가함(f/#이 증가함). 위쪽 렌즈는 f/2.8로 설정되어 있고 아래쪽 렌즈는 f/8로 설정되어 있음.

표 1은 녹색광(520nm)을 이용해 서로 다른 f/#로 계산한 Airy disk의 직경을 보여줍니다. 감지 가능한 최소 스폿 크기는 작은 크기의 픽셀을 빠르게 초과할 수 있어 적용 가능한 수준의 콘트라스트를 가진 센서의 최대 분해능을 산출할 때 난관에 봉착할 수 있습니다. 또한, 이는 렌즈 설계상의 어떠한 제한 요소나 렌즈 부품 및 광학 어셈블리의 제작에 관련된 생산 오차도 감안하지 않음에 따라 물리적으로 감지 가능한 가장 작은 스폿을 만드는 능력 저하로 이어져 해상도 및 콘트라스트 수준의 감소를 유발할 수 있습니다.

f/#	Airy Disk Diameter [µm] at a Wavelength of 520nm
2	2.54
2.8	3.55
4	5.08
5.6	7.11
8	10.15
11	13.96
16	20.30

표 1: 최소 스폿 크기 혹은 Airy disk는 f/#에 비례하며 픽셀 크기를 빠르게 초과할 수 있음. 샘플 픽셀 크기는 Resolution(해상도) 편의 표 1 참조.

참고: 이는 완전히 이론적인 내용이며 광학 시스템의 한계를 이해하는 출발점입니다.

회절 한계

모든 렌즈에는 회절 한계(diffraction limit)로 알려진 Airy disk와 물리적 법칙에 따라 결정되는 상한 성능이 존재합니다. 이러한 한계는 렌즈의 이론적 최대 분해능 $ \left[ \small{\tfrac{\text{lp}}{\text{mm}}} \right] $이며 상한 성능에 한계가 없는 설계상 완벽한 렌즈라 하더라도 실제로는 여전히 회절 한계 성능을 보이게 됩니다.

회절 한계는 두 개의 Airy 패턴을 더 이상 구분할 수 없는 지점을 가리킵니다(Contrast(콘트라스트) 편의 그림 2). 회절 한계 해상도는 렌즈의 컷오프 주파수라고도 하며, 렌즈의 f/#와 파장을 사용하여 계산할 수 있습니다. f/#에 관한 자세한 내용은 f/#(Lens Iris/Aperture 설정) 편을 참조하세요.

(2)$$ \xi_{\small{\text{Diffraction Limit}}} = \frac{1}{\left( \text{f} / \# \right) \times \lambda} \times \left( \frac{1000 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} }{1\text{mm}} \right) $$

(2)

$$ \xi_{\small{\text{Diffraction Limit}}} = \frac{1}{\left( \text{f} / \# \right) \times \lambda} \times \left( \frac{1000 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} }{1\text{mm}} \right) $$

회절 한계에 도달하면 렌즈는 초과하는 주파수를 더 이상 분해할 수 없습니다. 표 2는 f/#가 주어졌을 때 0%에서의 콘트라스트에 대한 회절 한계를 보여줍니다. 이 숫자가 커보일 수 있으나 이론적인 수치에 불과하므로 이외의 여러 가지 요소들도 고려해야 합니다. 통상적으로 봤을 때 백그라운드에 내재된 노이즈로 인해 콘트라스트가 0%에 가까울 때 이미징 센서는 이미지의 정보를 재현할 수 없게 됩니다. 표준 이미징 센서로 감지가 가능하려면 일반적으로 콘트라스트가 10% 이상은 되어야 합니다. 이미징 상에서 발생하는 복잡한 문제를 피하기 위해서는 어플리케이션에 적합한 해상도에서 콘트라스트를 20% 이상으로 맞추는 게 바람직합니다. 또한, 제조 공차와 관련된 렌즈의 광학 수차 및 변동은 시스템의 성능을 저하시킵니다.