MTF(Modulation Transfer Function) 개요

구성 요소 | 이해하기 | 중요성 | 특성화

광학 설계자들이 광학 시스템의 성능을 비교하려고 할 때 일반적으로 사용하는 측정 방법은 MTF(Modulation Transfer Function)입니다. MTF는 구면 singlet 렌즈처럼 단순한 부품부터 다중 요소 텔레센트릭 이미징 렌즈 어셈블리처럼 복잡한 부품까지 사용됩니다. MTF의 중요성을 이해하기 위해서는 구성 요소, 중요성 및 특성화를 포함하여 MTF를 정의하기 위한 몇 가지 일반 원칙과 실제 사례를 고려해야 합니다.

MTF의 구성 요소

MTF를 제대로 정의하기 위해서는 먼저 이미지 성능을 실제로 특성화하는 데 필요한 두 가지 용어, 해상도와 콘트라스트를 정의해야 합니다.

해상도

해상도는 피사체의 디테일을 구별하는 이미징 시스템의 능력입니다. 종종 lp/mm 단위로 표현됩니다(예를 들어, 1lp는 일련의 검은 선 하나와 흰 선 하나로 이루어짐). 이 mm당 n줄 쌍의 측정값 $ \small{\left(\tfrac{\text{lp}}{\text{mm}}\right)} $은 주파수로 알려져 있습니다. 주파수의 역수는 분해된 두 선 사이의 간격을 mm 단위로 나타냅니다. 흰색과 검은색 막대가 같은 간격으로 번갈아 가며 배열된 막대 타깃(예: 1951 USAF 타깃 또는 Ronchi Ruling)은 시스템 성능을 테스트하는 데 적합합니다. 테스트 타깃에 대한 자세한 설명은 올바른 테스트 타깃 선택하기 편을 확인하세요. 모든 이미징 광학 부품에서 이러한 패턴을 이미징할 때는 선명했던 선 엣지가 어느 정도 흐려집니다(그림 1). 블러를 최소화하여 많은 디테일을 보여주는 것이 고해상도 이미지입니다. 반대로, 저해상도 이미지는 세밀한 디테일이 부족합니다.

그림 1: 저해상도 이미징 렌즈를 통과하기 이전(왼쪽)과 이후(오른쪽)의 선명한 선 엣지

lp라는 개념을 쉽게 이해하려면 카메라 센서의 픽셀로 생각하면 됩니다. 1lp는 두 개의 픽셀에 해당합니다(그림 2). 각 해상도의 1lp마다 두 개의 카메라 센서 픽셀이 필요합니다: 한 픽셀은 빨간색 선으로 표시된 것을, 다른 하나는 픽셀 사이의 빈 공간을 의미합니다. 앞서 언급한 비유에 따라 이제 카메라의 이미지 해상도를 픽셀 크기의 두 배로 정의할 수 있습니다.

그림 2: (a) lp가 분해되지 않은 이미징 시나리오와 (b) lp가 분해된 이미징 시나리오

이에 따라 피사체 해상도는 카메라 해상도와 이미징 렌즈의 주배율(PMAG)을 사용하여 계산됩니다(방정식 1 - 2). 유의해야 할 점은 이 방정식은 이미징 렌즈에서 해상도 손실이 전혀 발생하지 않는다고 가정한다는 것입니다.

(1)$$ \text{Object Resolution} \left[ \large{\unicode[arial]{x03BC}} \text{m} \right] = \frac{\text{Camera Resolution} \left[ \large{\unicode[arial]{x03BC}} \text{m} \right]}{\text{PMAG}} $$

(2)$$ \text{Object Resolution} \left[ \tfrac{ \text{lp} }{\text{mm}} \right] = \text{PMAG} \times \text{Camera Resolution} \left[ \tfrac{ \text{lp} }{\text{mm}} \right] $$

콘트라스트/변조

흰색 막대에 최대값을, 검은색 막대에 0을 할당하여 막대 타깃의 강도를 정규화한다고 생각해 보겠습니다. 이 값을 그래프로 표기하면 사각파로 나타나므로, 콘트라스트라는 개념을 더 쉽게 확인할 수 있습니다(그림 3). 수학적으로는 방정식 3을 사용하여 콘트라스트를 계산합니다.

(3)$$ \text{% Contrast} = \left[ \frac{I_{\text{max}} - I_{\text{min}}}{I_{\text{max}} + I_{\text{min}}} \right] $$

그림 3: 사각파로 표현된 콘트라스트

이 동일한 원리를 그림 1의 이미징 예제에 적용할 때, 이미징 전후의 강도 패턴을 볼 수 있습니다(그림 4). 콘트라스트/변조는 최소 및 최대 강도 값이 피사체 면에서 이미지 면으로 얼마나 충실하게 전달되는지로 정의할 수 있습니다.

콘트라스트와 이미지 품질 간의 관계를 이해하기 위해 그림 1 및 그림 4의 동일한 해상도를 가진 이미징 렌즈이나 더 큰 lp 주파수를 가진 피사체를 촬영한다고 생각해보겠습니다. 그림 5는 선의 공간 주파수가 증가함에 따라 이미지의 콘트라스트가 감소함을 보여줍니다. 이 효과는 동일한 해상도의 이미징 렌즈로 작업할 때 항상 나타납니다. 이미지가 명확하게 보이기 위해서는 흑백이 분명해야 하며, 그 사이의 그레이스케일은 최소화해야 합니다.

그림 4: 막대 타깃과 해당 이미지의 콘트라스트

그림 5: 피사체 면과 이미지 면의 콘트라스트 비교

이미징 어플리케이션에서 이미징 렌즈, 카메라 센서, 조명은 최종 이미지 콘트라스트를 결정하는 데 중요한 역할을 합니다. 일반적으로 렌즈 콘트라스트는 재현되는 피사체 콘트라스트의 백분율로 정의됩니다. 센서의 콘트라스트 재현 능력은 일반적으로 아날로그 카메라에서는 데시벨(dB)로, 디지털 카메라에서는 비트로 지정됩니다.

MTF 이해하기

이제 MTF의 구성 요소인 해상도와 콘트라스트/변조가 무엇인지 확인했으므로 MTF 자체에 대해 알아보겠습니다. 이름에서 알 수 있듯이 렌즈의 MTF는 특정 해상도에서 콘트라스트를 피사체에서 이미지로 전달하는 능력을 측정하는 것입니다. 다시 말해, MTF는 해상도와 콘트라스트를 하나의 스펙으로 통합하는 방법입니다. 테스트 타깃에서 선 간격이 감소함에 따라(= 주파수가 증가함에 따라) 렌즈가 이러한 콘트라스트 감소를 효율적으로 전달하는 것은 점점 더 어려워집니다. 그 결과, MTF가 감소합니다(그림 6).

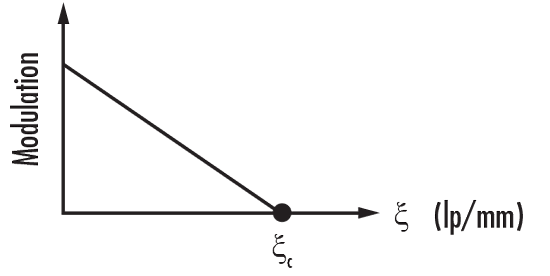
그림 6: 직사각형 조리개가 있는 무수차 렌즈의 MTF

원형 동공이 있는 무수차 이미지의 경우 MTF는 방정식 4로 계산되며, 여기서 MTF는 공간 해상도 $\small{\left( \xi \right)}$의 함수로, 시스템이 분해할 수 있는 가장 작은 lp를 나타냅니다. Cut-Off 주파수 $\small{\left( \xi _c \right)}$는 방정식 6으로 계산됩니다.

그림 6은 직사각형 동공이 있는 무수차 이미지의 MTF를 나타냅니다. 예상할 수 있듯이, 공간 해상도가 증가함에 따라 MTF가 감소합니다. 이는 최적의 경우를 예상한 것이며 어떠한 실제 시스템도 완전한 무수차는 아니라는 점에 유의해야 합니다.

(4)$$ \text{MTF} \left( \xi \right) = \frac{2}{\pi} \left( \varphi - \cos{\varphi} \cdot \sin{\varphi} \right) $$

(5)$$ \varphi = \cos ^{-1} \left( \frac{\xi}{\xi_c} \right) $$

(6)$$ \xi_c = \frac{1}{\lambda \cdot \left( f/ \# \right)} $$

MTF의 중요성

기존의 시스템 통합(그리고 덜 중요한 어플리케이션)에서는 가장 취약한 부분의 원리를 사용하여 시스템의 성능을 대략적으로 추정합니다. 가장 취약한 부분의 원리는 시스템의 해상도가 가장 낮은 해상도를 가진 부품에 의해서만 제한된다고 가정하는 것입니다. 이 접근 방식은 빠르게 추정할 때는 매우 유용하지만, 실제로는 결함이 있습니다. 가장 취약한 부분 하나만 이미지 품질을 저하시키는 것이 아니라 시스템 내의 모든 부품이 이미지 오류에 영향을 미치는 것이기 때문입니다.

시스템 내의 모든 부품은 관련 MTF를 가지고 있으므로 시스템의 전체 MTF에 영향을 미칩니다. 여기에는 이미징 렌즈, 카메라 센서, 이미지 캡처 보드, 비디오 케이블 등이 포함됩니다. 시스템의 최종 MTF는 해당 부품의 모든 MTF 곡선을 곱한 값입니다(그림 7). 예를 들어, Sony 흑백 카메라를 사용하여 두 렌즈의 시스템 성능을 평가함으로써 25mm 고정 초점 거리 렌즈와 25mm 더블 가우스 렌즈를 비교할 수 있습니다. 시스템 MTF 곡선을 분석하면 어떤 조합이 충분한 성능을 낼지 쉽게 판단할 수 있습니다. 예를 들어, 일부 계측 어플리케이션에서는 정확한 이미지 엣지 감지를 위해 일정량의 콘트라스트가 필요합니다. 최소 콘트라스트가 35%이어야 하고 필요한 이미지 해상도가 $ 30 \tfrac{\text{lp}}{\text{mm}} $이라면 25mm 더블 가우스 렌즈가 가장 좋은 선택입니다.

MTF는 해상도와 콘트라스트 측면에서 시스템의 전체 이미징 성능을 정량화하는 데 사용할 수 있는 최고의 도구 중 하나입니다. 따라서 설계자는 시스템 내 이미징 렌즈와 카메라 센서 각각의 MTF 곡선을 알면 특정 해상도에 맞춰 최적화할 때 적절한 선택을 할 수 있습니다.

그림 7: 시스템 MTF는 개별 부품의 MTF를 곱한 값: 렌즈 MTF x 카메라 MTF = 시스템 MTF

MTF의 특성화

실제 MTF 파악하기

이론적인 MTF 곡선은 렌즈의 광학 prescription을 바탕으로 생성할 수 있습니다. 이 이론적인 값이 도움이 될 수는 있지만 제조 공차를 고려한 후의 실제 렌즈 성능을 나타내는 것은 아닙니다. 제조 공차로 인해 원래의 광학 설계에서 약간의 성능 손실이 항상 발생하기 마련입니다. 기하 및 코팅 같은 요소들이 최적화된 렌즈나 렌즈 시스템에서 살짝 벗어나기 때문입니다. 이러한 이유로 에드몬드옵틱스는 제조 현장에서 MTF를 정량화하기 위한 광학 테스트 및 측정 장비에 투자하고 있습니다. 이 MTF 테스트 및 측정 장비를 통해 설계 렌즈와 상용 렌즈(광학 prescription이 공개되지 않은 경우)의 실제 성능을 특성화할 수 있습니다. 그 결과, 이전에는 prescription이 알려진 렌즈에 한정되었던 정밀 통합에 이제 상용 렌즈까지 포함할 수 있게 되었습니다.

MTF 그래프/데이터 판독

MTF 곡선 아래의 면적이 더 넓다고 해서 항상 최적의 선택이 되는 것은 아닙니다. 설계자는 사용 중인 어플리케이션의 해상도를 기준으로 결정해야 합니다. 앞서 설명한 바와 같이 MTF 그래프는 cycles/mm 대비 전달된 콘트라스트의 비율을 표시합니다. 에드몬드옵틱스가 제공하는 MTF 곡선에 대해 몇 가지 유의해야 할 사항이 있습니다.

각 MTF 곡선은 공간의 단일 포인트에 대해 계산됩니다. 일반적인 필드 포인트에는 정축(on-axis), 70% 필드, 풀 필드가 포함됩니다. 70%는 전체 이미징 영역의 약 50%를 캡처하기 때문에 흔히 사용되는 기준점입니다.
비축(off-axis) MTF 데이터는 tangential 및 sagittal 케이스 모두에 대해 계산됩니다(각각 T와 S로 표시됨). 때로는 두 개의 개별 곡선이 아니라 두 곡선의 평균이 제시되기도 합니다.
MTF 곡선은 시스템 공액, 파장 대역, f/#와 같은 여러 요인에 따라 달라집니다. MTF 곡선은 각각의 지정된 값에서 계산됩니다. 따라서 특정 어플리케이션에서 부품이 작동할지 여부를 판단하기 전에 이러한 요소들을 검토하는 것이 중요합니다.
공간 주파수는 cycles/mm(= lp/mm)로 표현됩니다. 이 주파수의 역수는 lp(검은색 막대 하나와 흰색 막대 하나의 사이클)의 간격을 밀리미터 단위로 산출합니다.
공칭 MTF 곡선은 광학 설계 프로그램에서 제공하는 표준 prescription 정보를 사용하여 생성됩니다. 이 prescription 정보는 글로벌 웹사이트, 인쇄 카탈로그 그리고 Zemax®에 제공된 렌즈 카탈로그에서도 확인할 수 있습니다. 공칭 MTF는 최상의 시나리오를 나타내며 제조 공차를 고려하지 않습니다.

개념적으로, MTF는 이해하기 어려울 수 있습니다. 피사체에서 이미지 면으로 콘트라스트를 전달하는 이 개념을 가장 쉽게 이해하려면 실제 사례를 살펴보는 것이 가장 좋은 방법일 수 있습니다. 그림 8 - 12는 두 개의 25mm 고정 초점 거리 이미징 렌즈에 대한 MTF 곡선과 이미지를 비교합니다. 이 두 렌즈는 각각 Finite Conjugate Micro-Video Lens(#54-855)와 Compact Fixed Focal Length Lens(#59-871)입니다. 그림 8은 이 두 렌즈의 다색 회절 MTF를 보여줍니다. 테스트 조건에 따라 두 렌즈 모두 동등한 성능을 발휘할 수 있습니다. 이 특정 예시에서는 둘 다 1951 USAF Resolution Target(그림 9)에서 그룹 2, 요소 5 - 6(그림 10에 빨간색 상자로 표시됨) 및 그룹 3, 요소 5 - 6(그림 10에 파란색 상자로 표시됨)을 분해하려고 시도합니다. 실제 피사체 크기 측면에서 그룹 2, 요소 5 - 6은 6.35 – $ 7.13\tfrac{\text{lp}}{\text{mm}} $ (14.03 - 15.75μm), 그룹 3, 요소 5 - 6은 12.70 – $ 14.25 \tfrac{\text{lp}}{\text{mm}} $ (7.02 - 7.87μm)을 나타냅니다. 주어진 요소 및 그룹 번호로 해상도를 쉽게 계산하려면 에드몬드옵틱스의 1951 USAF 해상도 기술 도구를 사용하십시오.

동일한 테스트 파라미터에서 #59-871(더 나은 MTF 곡선)이 #54-855에 비해 더 나은 이미징 성능을 제공한다는 것을 명확히 확인할 수 있습니다(그림 11 - 12). 이러한 특정 1951 USAF 요소를 사용하는 실제 사례에서 더 높은 공간 주파수에서의 더 높은 변조 값은 더 선명한 이미지로 귀결되지만, 항상 그러한 것은 아닙니다. 일부 렌즈는 상대적으로 낮은 공간 주파수를 매우 정확하게 분해할 수 있도록 설계되었으며, Cut-Off 주파수가 매우 낮습니다(즉, 상대적으로 높은 공간 주파수를 분해할 수 없음). 타깃이 그룹 -1, 요소 5 - 6이었다면 두 렌즈는 낮은 주파수에서의 변조 값을 고려할 때 훨씬 더 비슷한 이미지를 생성했을 것입니다.

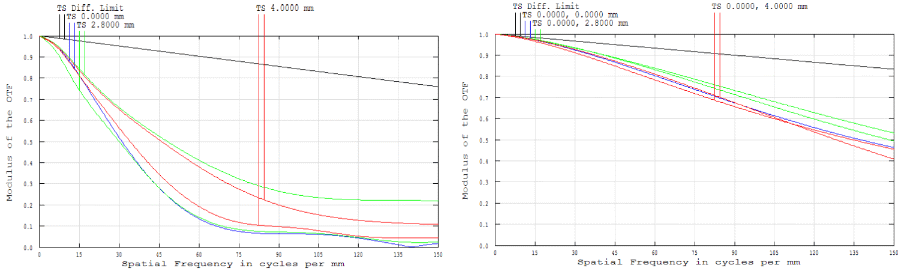
Finite Conjugate Micro-Video Lens 및 Compact Fixed Focal Length Lens의 다색 회절 MTF 비교

그림 8: Finite Conjugate Micro-Video Lens(#54-855, 왼쪽) 및 Compact Fixed Focal Length Lens(#59-871, 오른쪽)의 다색 회절 MTF 비교

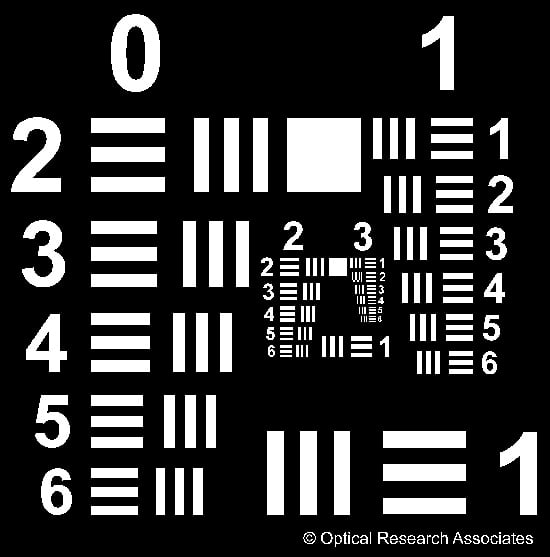
그림 9: 1951 USAF Resolution Target

1951 USAF Resolution Target에서 그룹 2, 요소 5 - 6(빨간색 상자) 및 그룹 3, 요소 5 – 6(파란색 상자)을 분해하는 Finite Conjugate Micro-Video Lens 및 Compact Fixed Focal Length Lens의 비교

그림 10: 1951 USAF Resolution Target에서 그룹 2, 요소 5 - 6(빨간색 상자) 및 그룹 3, 요소 5 – 6(파란색 상자)을 분해하는 Finite Conjugate Micro-Video Lens(#54-855, 왼쪽) 및 Compact Fixed Focal Length Lens(#59-871, 오른쪽)의 비교

1951 USAF Resolution Target에서 그룹 2, 요소 5 - 6을 분해하는 Finite Conjugate Micro-Video Lens 및 Compact Fixed Focal Length Lens의 비교

그림 11: 1951 USAF Resolution Target에서 그룹 2, 요소 5 - 6을 분해하는 Finite Conjugate Micro-Video Lens(#54-855, 왼쪽) 및 Compact Fixed Focal Length Lens(#59-871, 오른쪽)의 비교

1951 USAF Resolution Target에서 그룹 3, 요소 5 – 6을 분해하는 Finite Conjugate Micro-Video Lens 및 Compact Fixed Focal Length Lens의 비교

그림 12: 1951 USAF Resolution Target에서 그룹 3, 요소 5 - 6을 분해하는 Finite Conjugate Micro-Video Lens(#54-855, 왼쪽) 및 Compact Fixed Focal Length Lens(#59-871, 오른쪽)의 비교

MTF는 이미지 품질을 측정하는 데 사용되는 가장 중요한 파라미터 중 하나입니다. 광학 설계자 및 엔지니어는 특히 특정 피사체를 얼마나 정확하게 이미징하는지에 따라 성공 여부가 결정되는 어플리케이션에서 MTF 데이터를 자주 참조합니다. MTF를 제대로 이해하려면 먼저 해상도와 콘트라스트의 개념은 물론 피사체의 이미지가 피사체에서 이미지 면으로 어떻게 전달되는지에 대해서도 이해할 필요가 있습니다. 처음에는 어렵지만 MTF 데이터를 이해하고 궁극적으로 해석하는 것은 모든 광학 설계자에게 매우 강력한 수단이 됩니다. 지식과 경험을 바탕으로 MTF를 활용하면 수많은 제품들 속에서 적절한 렌즈를 선택하는 것이 훨씬 더 쉬워질 수 있습니다.

참고 문헌

Dereniak, Eustace. "OPTI 340 - Optical Design." Lecture, The University of Arizona, Tucson, AZ, Spring 2010.
Geary, Joseph M. "Chapter 34 – MTF: Image Quality V." In Introduction to Lens Design: With Practical Zemax Examples, 389-96. Richmond, VA: Willmann-Bell, 2002.
Hecht, Eugene. "11.3.5 Transfer Functions." In Optics, 550-56. 4th ed. San Francisco, CA: Addison-Wesley, 2001.
Smith, Warren J. "Chapter 15.8 The Modulation Transfer Function." In Modern Optical Engineering, 385-90. 4th ed. New York, NY: McGraw-Hill Education, 2008.

본 콘텐츠가 도움이 되었습니까?

본 콘텐츠를 평가해주셔서 감사합니다!