분산
광학 부품을 특히 레이저와 사용할 경우에는 광학 부품의 기판이 가지고 있는 특성에 더 많은 주의를 기울여야 합니다. 광학 부품용 기판에는 광학 글래스 및 수정 결정체와 같은 다양한 소재가 사용됩니다. 고객의 어플리케이션에 맞는 광학 부품을 선택하기 위해서는 제조 공정에서 발생할 수 있는 결함과 소재적 속성을 파악하고 있어야 합니다. 광학 기판의 주요 특성으로는 분산, 열흡수성, 균일성 등이 있으며, 기판 내부의 손상은 광학 부품에 사용되는 기판에 상당한 영향을 미칠 수 있습니다.
분산(dispersion)은 빛이 광주파수 및 파장과 같은 매개 변수 상에서 광학 매질을 투과할 때 위상 속도나 위상 지연에 의해 필연적으로 발생하는 속성입니다. 이러한 분산은 그림 1에서와 같이 색 분산, 모드간 분산, 편광 모드 분산 등의 다양한 유형으로 존재하며 레이저 광부품 표면의 내부에서 발생합니다.1
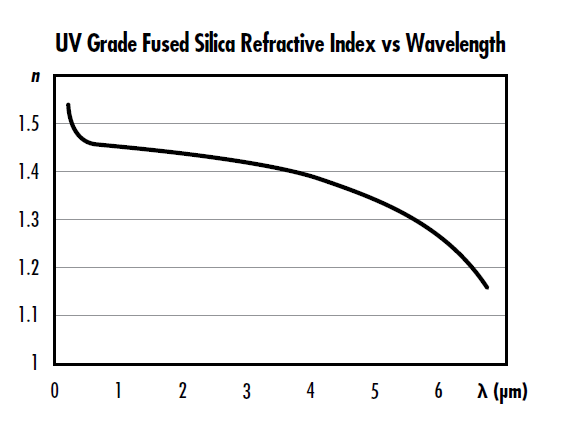
그림 1: 파장에 따른 UV 등급 용융 실리카의 굴절률
굴절률(refractive index)은 진공 상태에서의 빛의 속도와 공기나 글래스 등의 매질을 통과하는 동안 광파의 위상 속도 간 비율을 의미합니다. 펄스 레이저 용도에서 빛은 주파수로 설명하며, 일반적으로 시간이 더 중요하고 빛의 주파수는 고정된 값으로 주어지는 데 반해 파장은 내부에서 이동할 때의 굴절률에 따라 달라지기 때문입니다. 파장$ \small{\left( \lambda \right)} $은 다음과 같이 각도 주파수$ \small{\left( \omega \right)} $, 굴절률$ \small{\left( n \right)} $, 빛의 속도$ \small{\left( c \right)} $와 관련이 있습니다.
소재의 굴절률은 주로 셀마이어(Selmeier) 공식과 소재 상수 $\small{B_1}$, $\small{B_2}$, $\small{B_3}$, $\small{C_1}$, $\small{C_2}$, $\small{C_3}$를 이용해 설명할 수 있습니다.
색 분산(chromatic dispersion)은 빛의 파장에서 매질의 광 위상 속도 $\small{\nu _{p}}$에 의해 발생하며 대개 매질의 전자와 빛의 상호 작용으로부터 기인합니다. 색 분산은 $ \small{\lambda} $ $에 따른 굴절률의 첫 번째 편도함수 역수에 해당하는 아베수(그림 2)와 파장에 따른 굴절률의 두 번째 편도함수에 해당하는 부분 분산으로 설명됩니다.
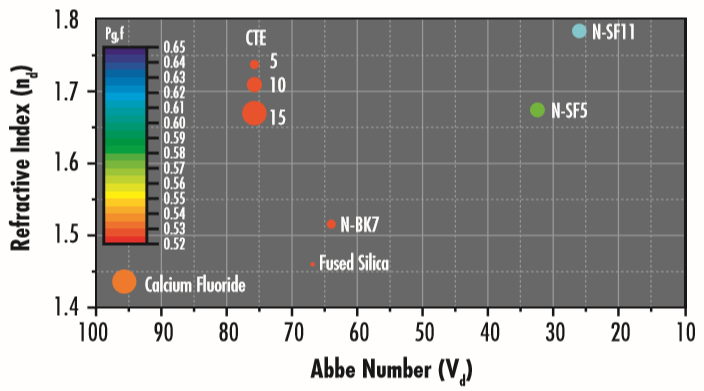
그림 2: 일반 글래스 유형의 굴절률 대 각각의 아베수를 보여주는 아베 다이어그램 도표. 열팽창 계수(CTE: coefficient of thermal expansion)의 정의는 당사 어플리케이션 노트 광학 기판의 열적 속성 편에서 자세히 다룸.
아베수는 다음과 같이 구할 수 있습니다.
여기서 $\small{n_D} $, $\small{n_F} $, $\small{n_C} $는 Fraunhofer D- $\small{\left( 589.3 \text{nm} \right)}$, F- $\small{\left( 486.1\text{nm} \right)}$, C- $\small{\left( 656.3 \text{nm} \right)}$ 스펙트럼 라인 파장에서 기판의 굴절률을 가리킵니다. 또한 파장에 따른 굴절률의 도함수를 이용하면 어느 파장에서도 소재의 아베수를 기술할 수 있습니다.
레이저 용도에서의 주된 관심사는 분산이 매질을 통과하는 레이저 펄스에 영향을 미치는 방식으로서 파수(wavenumber)에 따라 광 위상의 속도 변화를 가리키는 군속도 $ \small{ \left( \nu _g \right) } $ 로 설명할 수 있습니다.
파수$ \small{\left( k \right)} $는 $ \tfrac{2 \pi}{\lambda} $ 이며 이 개념은 간혹 spectral phase라고도 불립니다. 다중 파장의 빛이 소재를 통과할 때 군속도의 주파수(혹은 파장) 의존성에 의해 짧은 파장보다는 더 긴 파장이 다소 빠르게 이동하는 것이 일반적인 현상입니다2. 이러한 속도차는 프리즘을 통과하는 빛이 소재의 스펙트럼 분산으로 인하여 각 요소의 색상으로 분리되는 것과 동일한 방식으로 웨이브프론트 위상의 스펙트럼 변화를 일으킵니다. 그룹 속도는 주파수에 따른 위상 속도의 첫 번째 도함수로 구할 수 있으며 이때 군속도 분산($ \small{\text{GVD}} $: group velocity dispersion)은 주파수에 대한 군속도의 역수의 도함수입니다.
그룹 속도는 파장이나 주파수를 이용해 굴절률의 일차 도함수로 구할 수 있다는 점에서 스펙트럼 분산과 유사하며 $ \small{\text{GVD}} $는 파장이나 주파수를 이용하는 이차 도함수라는 점에서 부분 분산(partial dispersion)과 유사하게 활용됩니다. $ \small{\text{GVD}} $가 낮은 옵틱을 설계하는 작업은 뛰어난 색채 성능을 위한 설계 작업과 비슷합니다. 단, 아베수와 부분 분산보다는 군속도와 $ \small{\text{GVD}} $에 중점을 둡니다.
$ \small{\text{GVD}} $는 파장의 영향을 크게 받으며 주로 $ \tfrac{\text{fs}^2}{\text{mm}} $ 단위로 표기됩니다. 예를 들어 용융 실리카의 $ \small{\text{GVD}} $는 $ \small{589.3} \text{nm} $에서 $ +57 \tfrac{\text{fs}^2}{\text{mm}} $이며 $ \small{1500 \text{nm}} $에서는 $ -26 \tfrac{\text{fs}^2}{\text{mm}} $입니다. 이러한 파장 사이(대략 $ \small{1.3 \text{µm}} $)에는 $ \small{\text{GVD}} $가 0인 제로 분산 파장이 존재합니다. 그림 3은 용융 실리카의 파장 대비 $ \small{\text{GVD}} $에 관해 보여줍니다. 광섬유 통신에서의 $ \small{\text{GVD}} $는 일반적으로 주파수 대신에 파장에 의해 유도된 것으로 규정되며 주로 $ \tfrac{\text{ps}}{\left( \text{nm} \, \text{km} \right)} $의 단위로 표기됩니다.
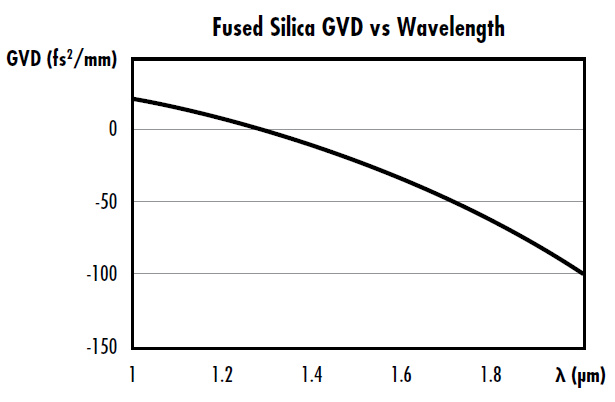
그림 3: 대략 $ \small{1.3 \text{µm}} $에서 제로 분산 파장을 가지는 용융 실리카의 $ \small{\text{GVD}} $ 대 파장
그림 3에서는 파장에 의한 $ \small{\text{GVD}} $ 의 변화량이 눈에 띄게 많다는 것을 알 수 있습니다. 쇼트 펄스는 본래 스펙트럼이 넓기 때문에 지속 시간이 대략 $ \small{30 \text{fs}} $ 미만인 극히 짧은 지속 시간의 레이저 펄스에서는 매우 큰 문제가 될 수 있습니다. 뿐만 아니라 색 분산은 광학 표면에서 굴절각이 주파수의 영향을 받도록 하기 때문에 각도 분산과 주파수에 따라 광경로 길이의 차이를 유발할 수 있습니다. 이러한 점은 초고속 레이저 시스템과 같은 광대역 시스템에 상당한 영향을 미칩니다.
모드간 분산(intermodal dispersion)은 광학 주파수와 전파 모드 상에서 다중모드 광섬유처럼 도파로(waveguide) 내의 빛의 군속도에 의해 발생합니다.2 이러한 분산은 다중모드 광섬유 통신 시스템에서 데이터 전송 속도 또는 비트 전송률을 심각하게 제한합니다. 대신 단일모드 광섬유나 굴절률 프로파일이 포물선 형태인 다중모드 광섬유를 사용하면 모드간 분산을 방지할 수 있습니다.
편광 모드 분산(polarization mode dispersion)은 편광 상태에 따른 매질 내에서의 전파 특성에 의해 발생하며 데이터 전송 속도가 높은 단일 모드 광섬유 시스템과 연관성이 있을 수 있습니다. 이 세 가지 유형의 분산 모두 자유 공간 또는 광섬유 내에서 울트라쇼트 펄스의 일시적 확장이나 압축을 유발할 수도 있으며 잠재적으로는 이로 인해 분리된 펄스가 서로 혼합되어 인식이 불가능하게 될 수도 있습니다(그림 4).
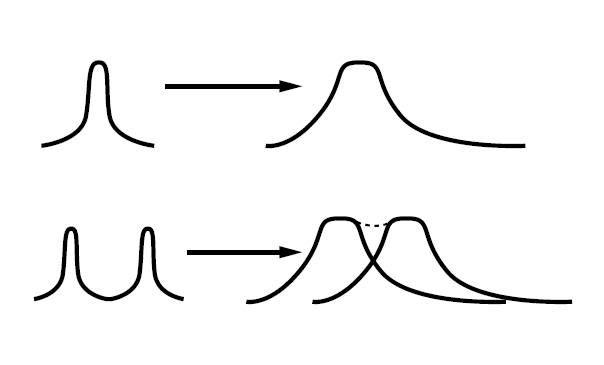
그림 4: 분산은 레이저 펄스가 광섬유를 따라 아래쪽으로 이동하도록 해 펄스를 알아볼 수 없을 때까지 확산시킴
참고 문헌
1 Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
2 Ghatak, Ajoy, and K. Thyagarajan. “Optical Waveguides and Fibers.” University of Connecticut, 2000.



























본사 및 지사별 연락처 확인하기
견적 요청 도구
재고 번호 입력 필요
Copyright 2023, 에드몬드옵틱스코리아 사업자 등록번호: 110-81-74657 | 대표이사: 앙텍하우 | 통신판매업 신고번호: 제 2022-서울마포-0965호, 서울특별시 마포구 월드컵북로 21, 7층 (서교동, 풍성빌딩)