온도 보정이 불필요한 비열화 개론

열화 디포커스 | achromatic & Athermal doublet 방정식 | 그래프를 통한 achrotherm 글래스 및 하우징 소재 선택 방법

온도 변화에 취약한 광학 시스템의 경우, 주변 환경으로 인한 열화 변형 및 이로 인해 야기되는 디포커스(defocus)부터의 영향을 덜 받을 수 있도록 비열식 광학 시스템의 개발이 무엇보다 중요합니다. 소재의 열팽창계수(CTE)와 온도별 굴절률 변화$ \left( \tfrac{\text{d}n}{\text{d}T} \right)$를 동시에 고려한 비열식 설계(athermal design)는 특히 적외선 스펙트럼에서 그 필요성이 더욱 증대됩니다. 대다수의 적외선(IR) 소재는 $ \tfrac{\text{d}n}{\text{d}T} $가 가시광선 유리의 온도별 굴절률 변화보다 수십 배 이상 크기 때문에 상당한 굴절률의 변화로 이어질 수 있습니다. 또한 광학 시스템은 주로 공기 중에서 설계되더라도, 하우징 소재는 열화에 민감하므로 비열식 설계를 고려할 때 이를 더욱더 주의해야 합니다.

열화 디포커스

온도 변화로 인한 소재의 팽창 및 수축은 소재의 열팽창계수인 $\small{\alpha}$에 의해 결정되며, 이 값은 $ \small{10^{-6}} \tfrac{\text{m}}{\text{K}} $, $ \small{10^{-6}} \tfrac{\text{m}}{˚ \text{C}} $,  $ \small{\tfrac{\text{ppm}}{\text{K}}} $, $ \small{\tfrac{\text{ppm}}{˚ \text{C}}} $와 같은 단위로 표기됩니다. 이때 온도 변화로 인한 소재의 길이$ \small{ \left( L \right)} $ 변화는 방정식 1을 통해 구할 수 있습니다.

열화로 인한 디포커스는 온도 변화로 광축상에서 초점 위치가 바뀌는 것으로서 온도 $ \left( \tfrac{\text{d}n}{\text{d}T} \right) $에 따른 굴절률의 변화와 소재의 팽창으로부터 기인합니다. 온도에 따라 공기 중에서 렌즈의 초점 거리 변화를 정량화하는 것과 유사한 공식은 방정식 2와 같으며, 여기서 $ \small{\beta} $는 열광학계수(therm-optic coefficient)를 가리킵니다.

방정식 3을 사용하면, $ \small{\beta} $를 정의할 수 있으며, 여기서 $ \small{\alpha_g} $는 유리의 열팽창계수(CTE)를 가리킵니다. $ \small{\beta} $를 구하는 방정식에는 매질이 공기일 때 온도별 굴절률 변화에 대한 항이 포함되어야 하지만, 이러한 항은 적외선 소재의 $ \left( \tfrac{\text{d}n}{\text{d}T} \right) $ 값에 비해 수치가 작으므로 해당 방정식에는 포함되지 않았습니다. 열광학계수는 적외선보다 공기 중에서 더 많은 영향을 받으며, 이에 따라 가시광에서는 근사치를 사용하지 않도록 주의해야 합니다.

방정식 4와 그림 1에서와 같이 열팽창계수가 $ \small{\alpha_h} $인 하우징에 장착된 렌즈의 초점 위치 변화는 하우징 팽창으로 인한 렌즈의 초점 거리 변화와 이미지 면의 위치 변화로 야기됩니다. 따라서 하우징 길이의 변화가 렌즈로 인한 초점 변화와 동일해야만, 디포커스가 0이 됨에 따라 이러한 시스템을 비열식 시스템으로 간주할 수 있습니다.

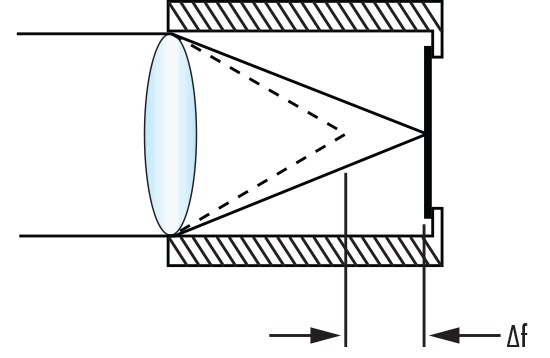
그림 1: 온도 변화 $ \small{ \left( \Delta f \right)} $로 인하여 금속 하우징에 장착된 렌즈에 Defocus$ \small{ \left( \Delta T \right)} $ 발생

Achromatic & Athermal Doublet 방정식

일반적으로 사용되는 광학 부품인 achromatic doublet은 각기 다른 소재의 양의 요소와 음의 요소로 구성된 렌즈로서 색수차의 양은 같지만 서로 상반된 색수차를 이용해 색상을 보정합니다. 광학 요소가 공기 중에 있다고 가정할 때, 최장 파장, 최단 파장, 중파장으로 정의되는 임의의 파장대역에 대한 $\small{{\nu}}$-넘버(역분산)는 방정식 5를 통해 구할 수 있습니다. 방정식 6과 7을 충족하면, 결과적으로 achromatic doublet이 생성됩니다. 최적의 솔루션은 $\small{{\nu}}$-넘버의 차이($\small{{\nu}}$)가 가장 큰 두 개의 광학 요소를 사용하는 것입니다.

최적의 솔루션은 $\small{{\nu}}$-넘버의 차이($\small{{\nu}}$.)가 가장 큰 두 개의 광학 요소를 사용하는 것입니다. 글래스 맵을 참고하면, $\small{\nu}$-넘버의 차이가 큰 crown 및 flint glass를 쉽게 선택할 수 있습니다. Athermal doublet을 설계할 수 있는 이와 유사한 방식은 당사의 색보정 방정식에서 일반적으로 광열 $\small{\nu}$ 넘버로 불리우는 열광학계수(방정식)의 역수(방정식)를 사용하는 것입니다(방정식 8 및 9). Doublet 설계 시 achromatic doublet 방정식과 athermal doublet 방정식을 모두 충족하면, 결과적으로 색보정과 비열 성능을 둘 다 갖춘 achrothermic 시스템이 생성됩니다(방정식 10).

광열 $\small{\nu}$-넘버 $ \small{\left( \nu_T \right)} $  vs. 컬러 $\small{\nu}$-넘버를 그래프로 표기하면, achrothermic 시스템을 개발하는 데 사용할 수 있는 두 가지 소재를 시각적으로 식별할 수 있습니다. 라인 방정식($ \small{y = mx + b} $,$ \small{m} $은 기울기, $ \small{b} $는 y-절편)이 주어진 상태에서, y-절편을 0으로 설정한 뒤 소재 $ \left( \nu_1, \, \nu_{T1} \right) $ 를 선택하면, 기울기(slope)는 $ \small{m} = \tfrac{\nu_{T1}}{\nu_1} $과 같이 구해집니다. 색수차와 비열화 성능을 달성하기 위해서는 doublet achrotherm 방정식으로부터 두 가지 소재의 기울기가 서로 동일해야 한다는 것을 파악하였습니다. 즉, 원점을 통과하는 선에 의해 두 소재가 연결될 수 있어야만 achrothermic 솔루션이 성립된다는 것을 알 수 있습니다. 그림 2에서 볼 수 있듯이 IG5와 AMTIR1은 공기 중에서 LWIR(8 - 12μm)에 대한 near-achrothermic 솔루션을 제공합니다. 참고: 해당 그래프는 시스템에 장착된 기계적 하우징에 대한 팽창 여부를 고려하지 않았음을 유의하십시오.

그림 2: LWIR(8-12μm)에서 $ \small{\nu_T} $ vs. $ \small{\nu} $를 비교한 샘플 차트

그래프를 통한 achrotherm 글래스 및 하우징 소재 선택 방법

광열 $\small{\nu}$-넘버 $\left( \small{\nu_T} \right) $ vs. 컬러 $\small{\nu}$-넘버를 그래프로 설명하는 방법 외에도, 광열 계수$\left(  \small{\beta} \right) $ vs. 컬러 $\small{\nu}$-넘버의 역수를 그래프로 설명하는 대체 방법이 있습니다.¹ 이러한 방식은 적용 가능한 두 가지 광학 소재를 확인하는 데 도움이 될 뿐 아니라, achrothermic 솔루션에 하우징을 장착해야 할 때 하우징 소재의 열팽창계수(CTE)를 확인하는 데도 도움이 됩니다 그림 3에서 볼 수 있듯이, y-절편은 두 가지 소재를 통해 연장되고 y-축을 교차하는 선을 통해 하우징에 필요한 소재를 알려줍니다. 필수 열팽창계수를 갖춘 단일 하우징 소재를 사용할 수 없는 경우 바이메탈 하우징 또는 이를 대체할 만한 메커닉 마운팅 솔루션을 사용하여 원하는 열팽창계수를 달성할 수 있습니다.

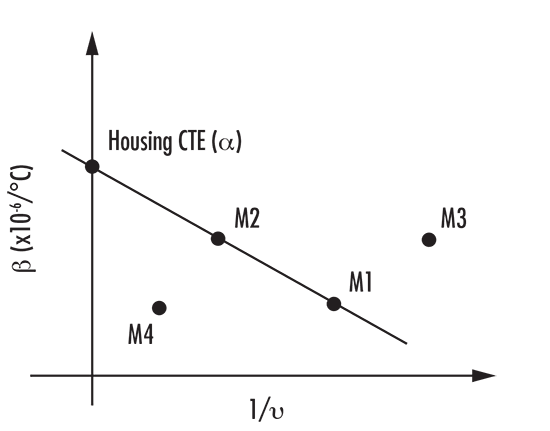
그림 3: $ \small{\beta} $ vs. $ \tfrac{1}{\nu} $를 그래프로 나타낸 일반적인 Athermal Glass Map

여기서 유의해야 할 점은 공기의 $ \tfrac{\text{d}n}{\text{d}T} $이 여전히 광학 소재의 $ \tfrac{\text{d}n}{\text{d}T} $에 비해 작다고 가정하는 것입니다. 적외선 시스템에서는 이러한 가정이 사실에 해당하지만, 가시광 스펙트럼에서 작동하는 시스템의 경우 공기의 $ \tfrac{\text{d}n}{\text{d}T} $를 반드시 고려해야 합니다. 비열화와 관련된 보다 자세한 사항 및 관련 공식은 다음의 방정식 및 참고 문헌을 통해 확인하기 바랍니다

참고: 위 방정식의 경우 시스템내 광소자의 배율은 사용 중인 파장대역의 중심에 위치하며, 적용된 굴절률은 기준 파장에 위치합니다

참고 문헌

• Schwertz, Katie, Dan Dillon, and Scott Sparrold. "Graphically Selecting Optical Components and Housing Material for Color Correction and Passive Athermalization." SPIE Proceedings Vol. 8486: Current Developments in Lens Design and Optical Engineering XIII, October 11, 2012.
• Schwertz, Katie, Adam Bublitz, and Scott Sparrold. "Advantages of Using Engineered Chalcogenide Glass for Color Corrected, Passively Athermalized LWIR Imaging Systems." SPIE Proceedings Vol. 8353: Infrared Technology and Applications XXXVIII, May 31, 2012.

문헌자료 편집자

¹  Tamagawa, Yasuhisa, Satoshi Wakabayashi, Toru Tajime, and Tsutomu Hashimoto. "Multilens System Design with an Athermal Chart." Applied Optics 34, no. 33 (December 1, 1994): 8009- 013.