가우시안 빔의 전파

본 내용은 레이저 옵틱스 리소스 가이드의 단원 5.1에 해당합니다.

다수의 레이저 광학 어플리케이션에서 레이저 빔은 이상적인 가우시안 분포를 나타내는 방사조도 프로파일을 가진 가우시안 빔이라고 가정합니다. 하지만 실제 모든 레이저 빔은 이상적인 가우시안 빔의 특성과 다소 차이를 보입니다. Beam quality factor로도 알려진 M² 를 이용하여 회절 한계에서의 가우시안 빔의 성능과 실제 레이저 빔의 성능을 비교할 수 있습니다(단원 6, 40-43쪽 참조).¹ 가우시안 방사조도 프로파일은 빔의 중앙 부분을 중심으로 대칭 구조를 이루며 빔의 중심으로부터 전파 방향에 수직한 거리가 멀어질수록 감쇠합니다(그림 1). 이러한 빔의 분포는 방정식 1을 통해 설명할 수 있습니다.²

(1)$$ I \! \left( r \right) = I_0 \exp{\left( \frac{-2 r^2}{w \! \left( z \right)^2} \right)} = \frac{2P}{\pi w \! \left( z \right)^2} \exp{\left( \frac{-2 r^2}{w \! \left( z \right)^2} \right)} $$

방정식 1에서 I₀은 빔의 중심에서 최대 방사조도, r은 광축에서 떨어진 반경 거리, w(z)는 방사조도가 I₀의 1/e²(13.5%)일 때 레이저 빔의 반경, z는 웨이브프론트가 평평할 때 평면에서부터 전파되는 거리, P는 빔의 총 출력을 가리킵니다.

그림 1: 가우시안 빔의 웨이스트는 방사조도가 최대치의 1/e<sup>2</sup> (13.5%)일 때의 위치로 정의됨

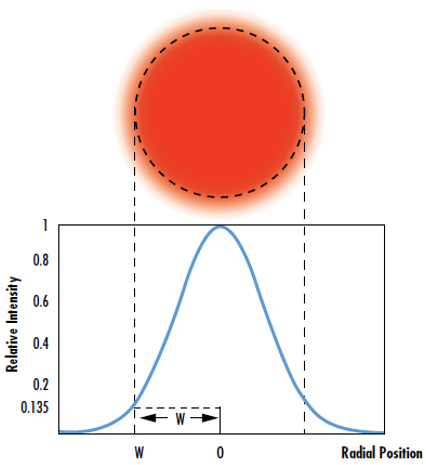
그림 1: 가우시안 빔의 웨이스트는 방사조도가 최대치의 1/e² (13.5%)일 때의 위치로 정의됨

그러나 빔이 전파할 때 방사조도 프로파일이 일정하지 않은 이유는 w(z)가 z의 영향을 받기 때문입니다. 회절로 인하여 가우시안 빔은 빔의 직경이 최소 수치에 도달하는 영역이자 beam waist (w₀)라고 불리는 곳에서 수렴하고 분산합니다. 이처럼 빔의 수렴 및 분산은 발산각 θ에 의해 빔 웨이스트의 양쪽에서 동일하게 일어납니다(그림 2). 빔 웨이스트와 발산각은 둘 다 광축과의 관계를 통해 산출되며 방정식 2와 3에서 확인할 수 있습니다.²:

(2)$$ w_0 = \frac{\lambda}{\pi \theta} $$

(3)$$\theta = \frac{\lambda}{\pi w_0} $$

위 방정식에서 λ는 레이저의 파장 그리고 θ는 원거리장(far field)의 발산각 근사치를 가리킵니다. 이에 따라 θ가 빔 웨이스트에 가까이 있는 빔의 발산을 정확하게 나타내지는 않지만 빔 웨이스트로부터의 거리가 멀어질수록 정확성은 높아집니다. 방정식 3에서 볼 수 있듯이 빔 웨이스트가 작을 경우에는 발산각이 더욱 커지며 빔 웨이스트가 클 경우에는 발산각이 더욱 줄어듭니다(또는 빔의 시준성 증가). 이는 곧 빔 익스팬더가 빔의 직경을 증가시켜야만 빔의 분산을 줄일 수 있음을 설명해줍니다.

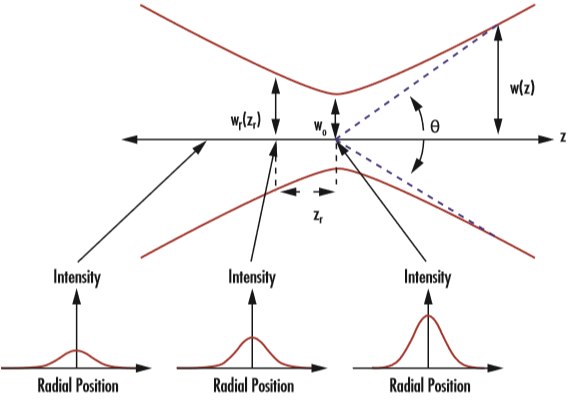
그림 2: 가우시안 빔은 빔 웨이스트(w0), 레일리 범위(z_R), 발산각(θ)에 의해 정의됨

빔 웨이스트 영역에서 빔의 직경 변화는 다음과 같이 정의됩니다.

(4)$$ w \! \left( z \right) ^2 = w^2 _0 + \theta ^2 z^2 = w^2 _0 + \left( \frac{\lambda}{\pi w_0 ^2} \right)^2 z^2 $$

(5)$$ w \! \left( z \right) = w_0 \sqrt{1 + \left( \frac{\lambda z}{\pi w_0 ^2} \right)^2} $$

가우시안 빔의 레일리(Raleigh) 거리는 빔의 횡단면이 두 배가 될 때의 z 값으로 정의됩니다. 이는 곧 w(z)가 √2w₀으로 증가할 때 발생합니다. 방정식 5를 이용하면 레일리 거리(z_R)를 다음과 같이 기술할 수 있습니다.

(6)$$ z_R = \frac{\pi w_0 ^2}{\lambda } $$

뿐만 아니라 w(z)는 z_R과도 연관성이 있습니다.

(7)$$ w \! \left( z \right) = w_0 \sqrt{1 + \left( \frac{\lambda z}{\pi w_0 ^2} \right)^2} = w_0 \sqrt{1 + \left( \frac{z}{z_R} \right)^2} $$

레이저의 웨이브프론트가 빔 웨이스트에서 평면이 되고 빔 웨이스트 영역에서부터의 거리가 증가하면 다시 원래의 형태에 가까워집니다. 이는 웨이브프론트의 곡률 반경이 무한대에 접근하기 시작하기 때문에 발생합니다. 웨이브프론트의 곡률 반경은 빔웨이스트에서 무한대로 시작하여 레일리 거리에서 최소가 되며, 광원에서 멀리 떨어지면 무한대로 돌아옵니다. (그림 3). 즉, 이러한 현상은 빔 웨이스트의 양쪽 모두에서 발생합니다.³

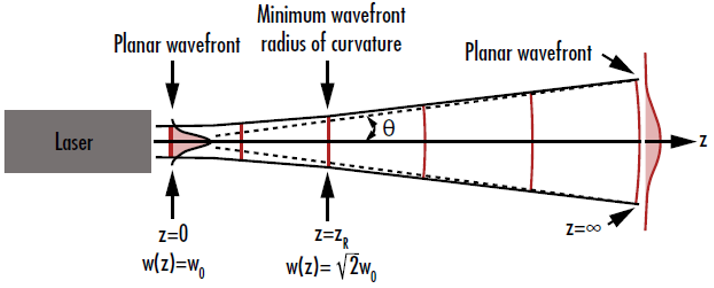
그림 3: 가우시안 빔의 웨이브프론트 곡률은 빔 웨이스트에 매우 가깝거나 멀리 떨어질 때 거의 무한대가 됨

가우시안 빔의 조작(manipulation)

다수의 레이저 광학 시스템에서는 단순히 "raw" 빔을 사용하는 대신 빔을 조작해가며 레이저 빔을 다룰 필요가 있습니다. 이처럼 빔을 조작하기 위해서는 렌즈, 미러, 프리즘 등의 광학 부품이 동원될 수 있습니다. 아래에서는 가우시안 빔을 조작하는 가장 일반적인 방법에 관해 안내합니다.

가우시안 빔의 Thin Lens 방정식

이상적인 thin lens의 특성은 다음의 방정식2을 통해 설명할 수 있습니다.²

(8)$$ \frac{1}{s'} = \frac{1}{s} + \frac{1}{f} $$

방정식 8에서 s’는 렌즈에서부터 이미지까지의 거리, s는 렌즈에서부터 피사체까지의 거리, f는 렌즈의 초점 거리입니다. 피사체와 이미지가 렌즈의 반대편에 있을 때 s는 음수 값, s’는 양수 값이 됩니다. 이 방정식에서는 렌즈의 실제 두께를 고려하지 않기 때문에 산출되는 값은 실제에 가까운 단순 근사치에 불과합니다(그림 4). 이외에도 thin lens 방정식은 방정식의 양쪽에 f를 곱하여 무차원 형식으로도 기술할 수 있습니다.

(9)$$ \frac{f}{s'} = \frac{f}{s} + 1 \text{ or } \frac{1}{\left( \frac{s'}{f} \right)} = \frac{1}{\left( \frac{s}{f} \right)} + 1 $$

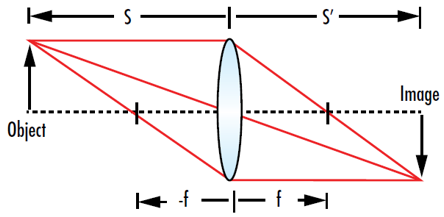
그림 4: 렌즈에서 피사체까지의 거리(s) 및 렌즈의 초점 거리(f)를 알면 thin lens 방정식을 이용해 이미지의 위치(s')를 구할 수 있음

Thin lens 방정식은 이미징 어플리케이션을 기술하는 것 외에도 입력빔의 웨이스트를 피사체로, 출력빔의 웨이스트를 이미지로 처리함에 따라 가우시안 빔의 포커싱에도 적용할 수 있습니다. 가우시안 빔은 광학 수차가 없는 이상적인 렌즈를 통과한 후에 가우시안 속성은 그대로 유지됩니다. 1983년에 시드니 셀프(Sidney Self)는 계산 시 가우시안 전파를 고려한 thin lens 방정식을 개발하였습니다.⁴

(10)$$ \boxed{ \frac{1}{s'} = \frac{1}{ s + \frac{z_R ^2}{\left( s + f \right)}} + \frac{1}{f} } $$

레이저에서부터 초점이 맺히는 스폿까지의 총 거리는 s’에 s의 절대값을 더해 계산됩니다. 방정식 10은 또한 양쪽에 f를 곱하여 무차원 형식으로도 기술할 수 있습니다.

(11)$$ \frac{f}{s'} = \frac{1}{\left( \frac{s}{f} \right) + \frac{\left( \frac{z_R}{f} \right)^2}{\left( \frac{s}{f} + 1 \right)} } + 1 $$

이 방정식은 zR/f가 0에 가까울 때 표준 thin lens 방정식과 유사함에 따라 초점 거리가 긴 렌즈에는 표준 thin lens 방정식을 사용할 수 있습니다. 방정식 방정식 10과 11을 활용하면 렌즈를 통해 이미징 처리가 된 후 빔 웨이스트의 위치를 알아낼 수 있습니다 (그림 5).

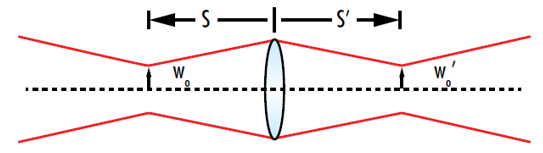
그림 5: 가우시안 빔의 초점을 다시 맞출 때 "피사체"가 입력 웨이스트, "이미지"가 출력 웨이스트가 됨

표준화된 이미지 거리(s’/f) 대 표준화된 피사체 거리(s/f)의 도표는 표준화된 레일리 거리(z_R/f)에서 출력 웨이스트가 존재할 수 있는 위치를 보여줍니다(그림 6). 이 도표에서는 렌즈를 통해 가우시안 빔을 포커싱하는 것과 기존의 thin lens로 이미징하는 것을 비교하면 몇 가지 중요한 차이가 있음을 알 수 있습니다. 가우시안 빔의 이미징은 이미지의 최대 및 최소 가능 거리를 둘 다 가지고 있지만, 기존의 thin lens는 최대 및 최소 가능 거리를 가지고 있지 않습니다. 다시 초점이 맞춰진 가우시안 빔의 이미지 거리는 -f와 반대인 -(f + z_R)의 피사체 거리에서 최대가 됩니다. 도표 상에서 s/f가 -1이고 s’/f가 1인 지점은 입력이 positive lens의 전면 초점에 위치할 때 출력은 렌즈의 후면 초점에 위치하게 됨을 가리킵니다.

Figure 6: z<sub>R</sub>/f가 0이면서 기존의 thin lens 방정식과 일치할 때의 곡선. 이 곡선은 z<sub>R</sub>/f가 0을 넘을 때 가우시안 이미지의 최소 및 최대 이미지 거리가 레일리 범위에 의해 정의됨을 나타냄

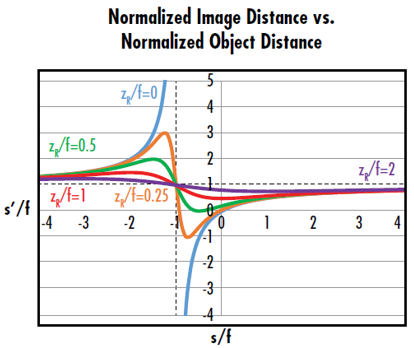
그림 6: z_R/f가 0이면서 기존의 thin lens 방정식과 일치할 때의 곡선. 이 곡선은 z_R/f가 0을 넘을 때 가우시안 이미지의 최소 및 최대 이미지 거리가 레일리 범위에 의해 정의됨을 나타냄

빔이 렌즈를 통과한 후 빔 웨이스트와 레일리 거리를 이해하기 위해서는 다음과 같이 계산되는 시스템 배율(α)에 대해 알고 있어야 합니다.

(12)$$ \alpha = \frac{w'_0}{w_0} = \frac{1}{\sqrt{1 - \left( \frac{s}{f} \right)^2 + \left( \frac{z_R}{f} \right)^2}} $$

이때 w₀는 렌즈를 통과하기 전의 빔 웨이스트, w₀’는 렌즈를 통과한 후의 빔 웨이스트입니다. 가우시안 빔의 thin lens 방정식은 렌즈를 통과한 후 빔의 릴레이 범위(z_R')를 포함시켜 다음과 같이 다시 기술할 수도 있습니다.

(13)$$ \boxed{ \frac{1}{ s' + \frac{{z'}_R ^2}{\left( s' - f \right)} } = \frac{1}{s} + \frac{1}{f} } $$

렌즈가 빔의 웨이스트에 위치한다면(s=0) 위 방정식은 더 이상 유효성을 발휘할 수 없습니다. 배율 상수를 제곱한 값의 역수는 빔의 웨이스트 크기와 위치³를 연관 지을 때 사용할 수 있습니다.

(14)$$ \frac{1}{\alpha ^2} = \frac{ \left| s \right| - f}{s' -f} = \left( \frac{w_0}{w'_0} \right)^2 $$

가우시안 빔을 스폿에 포커싱하기

레이저 소재 가공 또는 외과 수술 등의 다양한 용도에서 빔의 강도를 최대화하고 열에 영향을 받는 범위를 최소화하기 위해서는 가능한 가장 작은 스폿 크기로 레이저 빔의 초점을 맞추는 것이 무엇보다 중요합니다. 이와 같은 경우에는 목표를 대개 w₀'의 최소화에 둡니다(그림 7). 방정식 14를 개조한 버전은 출력 빔의 웨이스트를 최소화하는 방법³을 알아낼 때 사용할 수 있습니다.

(15)$$ \frac{\left( \left| s \right| -f \right)^2}{f^2 - \left( \frac{{w'}_0}{\theta} \right)^2 } = \left( \frac{w_{0}}{{w'}_0} \right)^2 $$

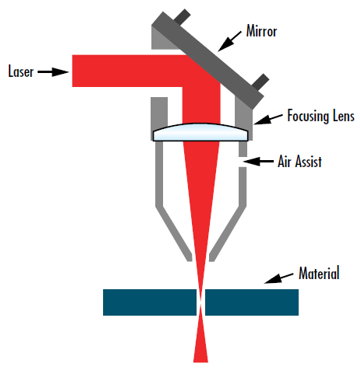
그림 7: 레이저 빔의 초점을 가능한 최소 크기로 맞추는 작업은 레이저 커팅을 포함한 다양한 용도에서 매우 중요한 부분을 차지함

방정식의 좌측에서부터 양쪽을 분모로 곱한 다음 (w₀')²로 곱하면 방정식 15는 다음과 같이 됩니다.

(16)$$ \left( \left| s\right| -f \right)^2 = f^2 \left( \frac{w_0}{w'_0} \right)^2 - \left( \frac{w_0}{\theta} \right)^2 = f^2 \left( \frac{w_0}{w'_0} \right)^2 - z_R ^2 $$

(17)$$ \left( w'_0 \right) ^2 \left[ \left( \left| s \right| - f \right)^2 + z_R ^2 \right] = f^2 w_0 ^2 $$

w₀'를 구하는 계산식은 다음과 같습니다.

(18)$$ \boxed{ w'_0 = w_0 \frac{f}{\sqrt{\left( \left| s \right| - f \right) ^2 + z_R ^2}} = \alpha w_0 } $$

(19)$$ \boxed{ \alpha = \frac{f}{\sqrt{\left( \left| s \right| -f \right)^2} + z_R ^2} } $$

렌즈의 초점 거리와 |s|-f를 줄이면 초점을 맺은 빔 웨이스트를 최소화할 수 있습니다. 방정식 18에서^w₀ 옆에 있는 항들은 빔이 렌즈를 통과한 후 입력빔의 값을 출력빔의 값과 비교해주는 또 다른 형식의 배율 상수 α로 정의됩니다(그림 8).³

(20)$$ \theta ' = \frac{\lambda}{\pi w'_0} = \frac{\lambda}{\pi \alpha w_0} = \frac{\theta}{\alpha} $$

(21)$$ z'_R = \frac{w'_0}{\theta '} = \frac{\alpha w_0}{\left( \frac{\theta}{\alpha} \right)} = \alpha ^2 z_R $$

(22)$$ \boxed{ s' = f + \alpha ^2 \left( \left| s \right| - f \right)} $$

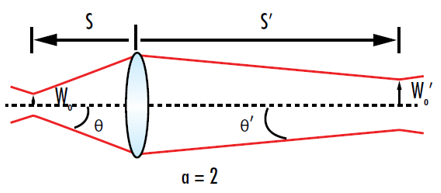
그림 8: 배율이 2일 때 출력빔의 웨이스트는 입력빔 웨이스트의 두 배가 되고 출력 분산은 입력 분산의 절반이 됨

출력빔의 웨이스트 크기와 위치를 더욱 단순하게 계산해내는 제한 사례로는 두 가지가 있습니다. 이 두 가지 사례는 s가 z_R보다 훨씬 작을 때 또는 s가 z_R보다 훨씬 클 때입니다.³ 그 다음 렌즈가 레이저의 레일리 거리 내에 있을 때 s << z_R과 (|s|-f)²<zR2이 성립됩니다. 방정식 19를 단순화하면 다음과 같습니다.

(23)$$ \alpha = \frac{f}{z_R} = \frac{f \theta}{w_0} $$

이는 또한 출력빔의 웨이스트, 발산각, 릴레이 거리, 웨이스트 위치에 대한 계산을 단순화합니다.

(24)$$ \theta ' = \frac{\theta}{\alpha} = \frac{ \theta w_0}{f \theta} = \frac{w_0}{f} $$

(25)$$ z_R ' = \alpha ^2 z_R = \frac{f^2}{z_R ^2} z_R = \frac{f^2}{z_R} $$

(26)$$ \boxed{ w'_0 = \alpha w_0 = f \theta } $$

(27)$$ \boxed{ s' = f + \alpha^2 \left( \left| s \right| - f \right) = f + \frac{ \left| s \right| f^2}{z_R ^2} \approx f } $$

s가 z_R보다 훨씬 작을 때 렌즈에서부터 초점이 맺히는 스폿까지의 거리는 렌즈의 초점 거리와 동일합니다.

렌즈가 레일리 거리를 멀리 벗어나고 s가 z_R보다 지나치게 큰 기타 제한적인 상황에서는 방정식 19를 다음과 같이 단순화해서 사용할 수 있습니다.

(28)$$ \alpha = \frac{f}{\left| s \right|} $$

출력빔의 웨이스트 직경은 다음과 같이 계산됩니다.

(29)$$ w'_0 = \frac{f w}{ \left| s \right|} $$

s가 z_R보다 훨씬 작을 때의 경우와 마찬가지로 출력빔의 웨이스트, 발산각 레일리 거리, 빔 웨이스트의 위치를 구하는 계산식 또한 단순화할 수 있습니다.

(30)$$ \theta ' = \frac{\theta}{\alpha} = \frac{\left| s \right| \theta }{f} $$

(31)$$ z'_R = \alpha^2 z_R = \frac{f^2 z_R}{s^2} $$

(32)$$ \boxed{ w'_0 = \alpha w_0 = \frac{fw_0}{\left| s \right|} } $$

(33)$$ \boxed{ s' = f + \alpha ^2 \left( \left| s \right| - f \right) = f + \frac{\left( \left| s \right| - f \right) f^2}{s^2} = f + \frac{f^2}{ \left| s \right|} \approx f } $$

s가 z_R보다 훨씬 클 경우 렌즈에서부터 초점이 맺히는 스폿까지의 거리는 렌즈의 초점 거리와 동일합니다.

빔의 웨이브프론트는 빔의 웨이스트로부터 매우 멀리 떨어진 지점에서 평면에 가깝기 때문에 이 두 가지 결과를 직관적으로 이해할 수 있습니다. 빔이 위치한 이들 지점에서 빔은 거의 완벽한 시준을 이룹니다(그림 9). 표준 thin lens의 방정식에 따르면 시준된 입력빔은 렌즈의 초점 거리와 동 동일한 상거리를 갖게 됩니다.

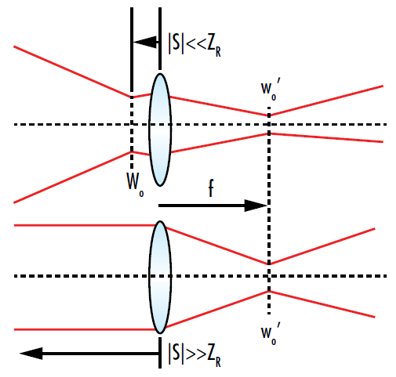
그림 9: 입력빔의 웨이스트가 렌즈에 매우 가깝거나 매우 멀리 떨어져 위치한 경우 가우시안 빔이 렌즈를 통과한 후 초점을 맺는 스폿은 렌즈의 초점에 위치하게 됨. 이는 입력빔이 해당 스폿에서 거의 시준 상태가 되기 때문임

가우시안 초점 이동

반비례적으로 렌즈에서부터 고정된 거리(L)에 위치한 목표물에 초점을 맺은 빔의 강도는 웨이스트가 목표물에 위치할 때 최대화가 되지는 않습니다. 실제로 목표물에서의 강도는 웨이스트가 목표물 이전 지점에 위치할 때 최대화가 됩니다(그림 10). 알려진 바에 의하면 이러한 현상을 바로 가우시안 초점 이동(Gaussian focal shift)이라고 합니다.

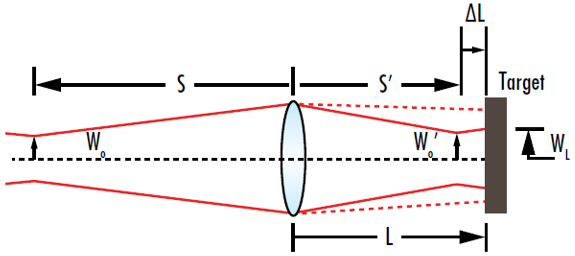
그림 10: 목표물에서 빔의 반경은 초점을 맺은 웨이스트가 목표물에 위치할 때가 아닌 목표물에 도달하기 전 특정 위치에서 최소화가 됨

본문에서는 가우시안 초점 이동의 어원에 관해 길게 다루지 않지만, 아래의 계산식을 이용하면 목표물에서 빔의 반경을 구할 수 있습니다.⁵

(34)$$ w_L = \frac{w_0}{z_R} \left[ f^2 - 2 \left( \left| s \right| - f \right) \left( L - f \right) + \left( \frac{L-f}{\alpha} \right)^2 \right] $$

포커싱 렌즈(f)의 초점 거리의 경우 방정식 34를 미분한 뒤 ^d⁄_df [w_L (f )]이 0일 때 f를 구하면 빔의 반경을 최소화하는 렌즈 초점 거리를 알아낼 수 있어 이를 이용해 목표물에서의 가장 높은 강도 또한 구할 수 있습니다.

(35)$$ \frac{ \text{d} }{ \text{d}f } \left[ w_L \! \left( f \right) \right] = \frac{w_0}{z_R} \left[ 2f + 2 \left( \left| s \right| -f \right) + \left( L - f \right) - \frac{2 \left( L - f \right)}{\alpha ^2} \right] $$

(36)$$ \frac{ \text{d} }{ \text{d}f } \left[ w_L \! \left( f \right) \right] = 0 \text{ when } f = \left( \frac{1}{\left| s \right| + \frac{z_R ^2}{\left| s \right|}} + \frac{1}{L} \right) ^{-1} $$

|s|가 0 또는 무한대에 근접하면 f가 L과 동일할 때 ^d⁄_df [w_L (f )]는 0이 됩니다. 이 두 가지 경우에서 다 입력빔은 거의 시준 상태가 됨에 따라 빔의 반경은 렌즈의 초점(focal point)에서 최소가 됩니다.

가우시안 빔의 시준(collimation)

사실상 발산각이 0인 빔을 시준하기란 불가능하지만 가장 가까운 빔의 웨이스트와 관측 지점 사이의 거리를 최대화하거나 발산각을 최소화함으로써 유사 시준 빔을 달성할 수 있습니다. 출력 발산각은 배율 상수 α에 반비례하기 때문에 출력 분산은 |s|= f가 성립될 때 최소값에 도달할 수 있습니다(그림 11).

그림 11: 가우시안 빔을 시준하기 위해서는 빔의 웨이스트에서부터 시준 렌즈까지의 거리가 렌즈의 초점 거리와 같아야 함

참고 문헌

Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
“Gaussian Beam Optics.” CVI Laser Optics, IDEX Optics & Photonics.
O'Shea, Donald C. Elements of Modern Optical Design. Wiley, 1985.
Self, Sidney A. “Focusing of Spherical Gaussian Beams.” Applied Optics, vol. 22, no. 5, Jan. 1983.
Katz, Joseph, and Yajun Li. “Optimum Focusing of Gaussian Laser Beams: Beam Waist Shift in Spot Size Minimization.” Optical Engineering, vol. 33, no. 4, Apr. 1994, pp. 1152–1155., doi:10.1117/12.158232.

이전 단원 다음 단원