빔의 품질 및 스트렐 비율

본 내용은 레이저 옵틱스 리소스 가이드의 단원 6.2, 6.3, 6.4과 6.5에 해당합니다.

레이저의 실제 성능과 품질을 정확하게 예측하기 위해서는 빔의 품질을 기술하는 M² 계수를 반드시 이해해야 합니다. 일단 레이저의 성능을 알고 있고 레이저와 함께 사용되는 광학 시스템의 실제 성능이 정의되면 최종 시스템의 성능을 파악할 수 있습니다. 광학 시스템의 실제 성능과 이상적인 성능을 비교하기 위해서는 스트렐 비율(Strehl ratio)을 이용해 회절 제한 성능 확인 작업을 거쳐야 합니다.

M² 계수

레이저 빔의 품질은 빔의 실제 형태를 가우시안 빔의 이상적인 형태와 비교할 때 사용하는 M² 계수(factor)에 의해 규정됩니다. ISO 표준 11146은 M²계수를 다음과 같이 정의합니다.¹

(1)$$ M^2 = \frac{\pi w_0 \theta}{\lambda} $$

방정식 1에서 w₀는 빔의 웨이스트, θ는 레이저의 발산각, λ는 레이저의 파장(그림 1)을 가리킵니다. 당사 어플리케이션 노트 가우시안 빔의 전파 편에서 정의된 바와같이 가우시안 빔의 발산각은 다음의 방정식을 따라 산출됩니다.

(2)$$ \theta = \frac{\lambda}{\pi w_0} $$

산출된 발산각을 방정식 1에 대입하면 가우시안 빔에 사용되는 M2 계수의 방정식을 단순화할 수 있습니다.

(3)$$ M^2 = \frac{\pi w_0}{\lambda} \times \frac{\lambda}{\pi w_0} = 1 $$

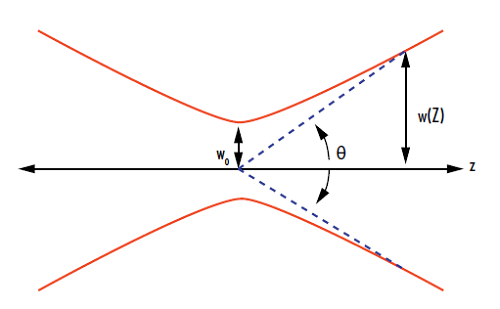
그림 1: Illustration of the divergence angle and beam waist of a laser beam

그림 1: 레이저 빔의 발산각과 빔 웨이스트의 도해

따라서 M² 계수가 1일 때는 회절한계에서의 가우시안 빔과 일치합니다. M²계수가 1보다 클 경우에는 이상적인 가우시안 빔에서 벗어난 것을 의미합니다. 1 미만의 계수는 산출이 불가능한 값입니다. 에르미트-가우시안 모드의 M² 계수는 x 방향에 있는 (2n + 1)과 y 방향에 있는 (2m + 1)에 의해 계산됩니다.² 예를 들어 TEM₁₃은 M² 계수가 x 방향에서는 3이 되고 y 방향에서는 7이 됩니다. 헬륨 네온 레이저는 일반적으로 1과 1.1 사이의 M² 계수를 가지고 있습니다.

레이저 빔의 광학 파워와 더불어 M² 계수는 빔의 방사조도(radiance)를 결정합니다. 또한 M² 계수는 레이저 파장을 당사 어플리케이션 노트 가우시안 빔의 전파 편의 모든 방정식에서 볼 수 있는 M² 계수로 곱한 파장으로 대체하여 빔이 전파할 때 빔 반경의 근사값을 구하는 데도 사용할 수 있습니다.³

M² 계수는 주어진 발산각에서 레이저 빔이 얼마나 수월하게 초점을 맞출 수 있는지를 알려주기 때문에 레이저 용도에서 매우 중요한 요소입니다. M² 계수가 낮다는 것은 더욱 조밀한 포커싱, 빔 내에서 더 효율적인 파워의 사용, 더 높은 잠재력의 레이저 유효 출력이 가능함을 의미합니다.

M²를 측정하는 것은 레이저 축에 있는 단일 평면에서 빔의 프로파일을 측정하는 것 만큼이나 간단한 일이 아닙니다. ISO 11146 규정에는 근거리 및 원거리장에 관계없이 광축을 따라 각기 다른 지점에서 빔의 반경을 5회 측정해야 한다고 기술되어 있습니다. TEM₀₀ 모드를 전혀 포함하지 않고도 어느 특정 평면에서 빔을 이상적인 가우시안 빔처럼 보이도록 만들 수는 있습니다(그림 2). 특정 평면에서 단면도가 완벽한 가우시안 분포처럼 보일지라도 빔은 가우시안 빔과는 매우 다른 양상으로 전파되고 더 큰 발산각을 갖게 될 것입니다. 각기 다른 평면에서 반지름을 여러 번 측정해야만 빔과 실제 가우시안 빔의 차이를 빠르게 확인할 수 있습니다. 측정된 빔의 반경(w(z))이 빔의 웨이스트(w₀), 파장(λ), M² 계수와 연관성이 있음은 다음의 방정식을 통해 설명할 수 있습니다.⁶

(4)$$ w \! \left( z \right) ^2 = w^2 _0 \left[ 1 + \left(z - z_0 \right)^2 \left( \frac{M^2 \lambda}{\pi w_0 ^2} \right)^2 \right] $$

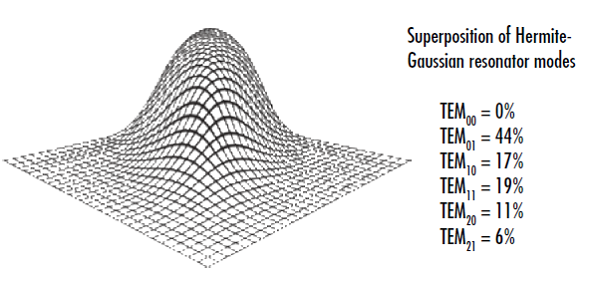
그림 2: 이와 같은 빔의 단면은 TEM00 모드를 포함하지 않더라도 특정 평면에서 가우시안 형태를 나타내며 레이저의 M<sup>2</sup> 계수를 구하기 위해서는 레이저 축을 따라 강도를 여러 번 측정하는 것이 중요함을 알 수 있음

그림 2: 이와 같은 빔의 단면은 TEM₀₀ 모드를 포함하지 않더라도 특정 평면에서 가우시안 형태를 나타내며 레이저의 M² 계수를 구하기 위해서는 레이저 축을 따라 강도를 여러 번 측정하는 것이 중요함을 알 수 있음

Beam Parameter Product

Beam parameter product (BPP)는 레이저 빔의 품질을 평가하기 위해 사용되는 또 다른 측정 지표로서 빔 웨이스트에서의 빔 반경과 1/2 빔 발산각의 곱으로 정의됩니다. BPP는 주로 mm mrad 단위로 표기되며 다음의 방정식과 같이 M² 계수와 관련이 있습니다.

(5)$$ \text{BPP} = \frac{M^2 \lambda}{\pi} $$

BPP는 M² 계수에 정비례함에 따라 BPP가 커질수록 빔의 품질은 낮아집니다. BPP의 최소값은 λ/π이며 이상적인 가우시안 빔에서만 최소값을 달성할 수 있습니다.

Power in the Bucket

Power in the bucket (PIB) 역시 빔의 품질을 정의하는 또 다른 측정 지표로서 대개 고출력 레이저 시스템과 소재 가공 용도에 사용됩니다. PIB는 가공 중인 소재의 표면에서 가장 흔히 발견되는 스폿의 특정 반경으로 지정되는 "bucket"에 걸쳐 얼마나 많은 레이저 출력이 결합되는 지를 나타냅니다. 겉보기에는 단순 개념일 수 있으나 특히 원거리장에서는 버킷의 형태를 더욱 정확하게 정의해야 하며 이상적인 시나리오와 비교하는 작업은 근거리장 레이저 빔 형태의 스펙에 따라 달라집니다.
PIB에 대한 업계 간의 정확한 표준이 존재하지 않지만, 대다수는 수직 또는 수평 빔의 품질로 보고됩니다.9⁷

(6)$$ \text{Vertical Beam Quality} = \sqrt{\frac{\text{Ideal Power in Bucket}}{\text{Actual Power in Same Bucket}}} $$

(7)$$ \text{Horizontal Beam Quality} = \frac{\text{Actual Beam Radius at a Given Power}}{\text{Ideal Beam Radius at the Same Power}} $$

M² 계수 및 BPP와 마찬가지로 PIB 값이 낮을수록 빔의 품질은 올라가게 됩니다. PIB는 정의된 "bucket"의 출력 함수를 λ/D 함수로 도식화해 시각적으로 표현할 수 있으며 이때 D는 근거리장 빔의 직경을 가리킵니다(그림 3). 수직 빔의 품질은 이상적인 가우시안 빔의 버킷에서의 출력 함수 비율 대비 주어진 λ/D에서의 실제 빔 출력 함수 비율에 대한 제곱근으로서 그래프의 수직 치수에 해당합니다. 마찬가지로 수평 빔의 품질은 이상적인 가우시안 빔의 λ/D 값 대비 버킷 내 주어진 출력 함수에서 실제 빔의 λ/D 값에 대한 비율이며 그래프의 수평 치수에 해당합니다.

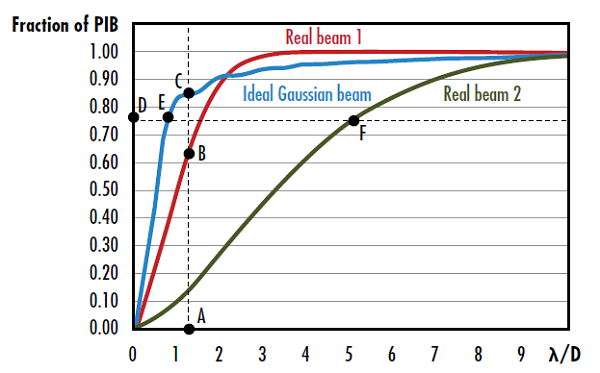
그림 3: 실제 빔 1의 수직 빔 품질은 세그먼트 AC 대 세그먼트 AB 비율의 제곱근으로 결정되며 실제 빔 2의 수평 빔 품질은 세그먼트 DF 대 세그먼트 DE의 비율로 결정됨7

그림 3: 실제 빔 1의 수직 빔 품질은 세그먼트 AC 대 세그먼트 AB 비율의 제곱근으로 결정되며 실제 빔 2의 수평 빔 품질은 세그먼트 DF 대 세그먼트 DE의 비율로 결정됨⁷

원형 대 타원형 빔

레이저 빔의 형태를 고려할 때는 레이저가 생성하는 빔이 원형인지 아니면 타원형인지 여부를 결정하는 것이 무엇보다 중요합니다. 반도체 레이저 다이오드는 활성 영역이 직사각 모양이기 때문에 x와 y 방향에서 발산 각도가 다른 타원형 모양의 빔을 방출합니다(그림 4). 작은 구경에서 더 큰 회절이 발생함에 따라 치수가 짧은 활성 영역에서 빔의 발산이 더 많이 일어나기 때문에 결국 비점수차가 존재하는 빔으로 이어지게 됩니다. 발산각이 큰 축은 fast axis로 정의되고 반면에 발산각이 작은 축은 slow axis로 정의됩니다. 타원형 빔은 원형 빔에 비해 초점이 맺히는 스폿의 크기가 크기 때문에 시스템 성능에 피해를 입힐 수 있습니다. 이는 스폿 크기가 클수록 원형 빔에 비해 방사조도가 낮아져 레이저에 더 높은 파워의 입력이 필요할 수 있기 때문입니다. 실린더 렌즈는 주로 타원형 빔을 원형화하는 데 사용됩니다(그림 5). 실린더 렌즈에 관한 내용은 실린더 렌즈 사용 시 고려해야할 점(84-85쪽) 편에서 자세히 다룹니다.

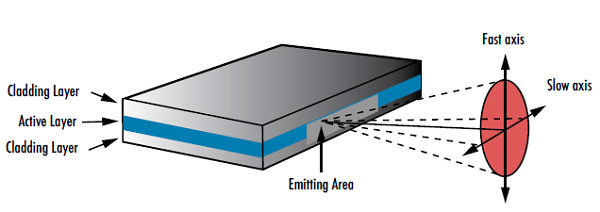
그림 4: 레이저 다이오드의 기하학적 구조에 의해 서로 다른 두 개의 발산각을 가지고 있는 타원형 빔이 형성됨

그림 5: 실린더 렌즈는 fast axis와 slow axis에서 각각 성능을 발휘함에 따라 타원형 빔을 원형 빔으로 전환하는 데 주로 사용됨

스트렐 비율

M² 계수로 레이저의 실제 성능과 이상적인 빔을 서로 비교할 수 있듯이 광학 시스템이나 부품의 스트렐 비율(Strehl ratio)은 실제 성능을 이상적인 성능과 비교할 때 사용됩니다. 구면 및 비구면 렌즈를 포함한 포커싱 옵틱의 스트렐 비율은 포인트 광원에서 실제 옵틱의 최대 초점 방사조도 대 이론적으로 회절 한계에서의 옵틱에 이상적인 최대 방사조도의 비율을 나타냅니다(그림 6).⁷ 스트렐 비율이 1이라는 것은 광학 수차가 발생하지 않는 완벽한 옵틱임을 가리킵니다. 광학 업계에서는 일반적으로 스트렐 비율이 0.8 이상일 때의 렌즈를 회절 제한 렌즈로 간주합니다.

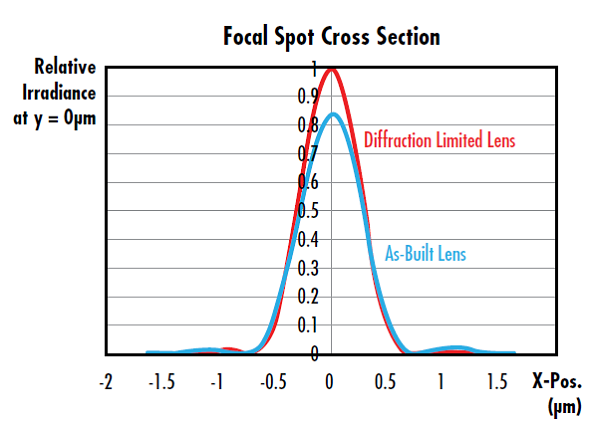
그림 6: 이 렌즈는 스트렐 비율이 0.8보다 큰 0.826으로서 회절 제한 렌즈로 간주됨

옵틱의 스트렐 비율은 방정식 8에 나와 있듯이 RMS 투과 웨이브프론트와 대략적으로 관련이 있습니다. 이때 S는 스트렐 비율, σ는 파동에서 옵틱의 RMS 웨이브프론트 에러를 가리킵니다.⁸ 이 근사치는 웨이브프론트 에러가 0.1 wave 이만일 때 유효합니다.

(8)$$ S = \exp{\left[ - \left( 2 \pi \sigma \right)^2 \right]} $$

옵틱 표면의 비균일도가 스트렐 비율에 미치는 영향은 비구면 렌즈의 비균일성과 스트렐 비율 편에서 상세히 다룹니다.

참고 문헌

International Organization for Standardization. (2005). Lasers and laser-related equipment – Test methods for laser beam widths, divergence angles and beam propagation ratios (ISO 11146).
A. E. Siegman, “New developments in laser resonators”, Proc. SPIE 1224, 2 (1990)
Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
International Organization for Standardization. (2005). Lasers and laser-related equipment — Test methods for laser beam widths, divergence angles and beam propagation ratios — Part 1: Stigmatic and simple astigmatic beams (ISO 11146-1:2005).
A. Siegman, “’Non-Gaussian’ Beam”, OSA Annual Meeting, Long Beach, CA (1997)
Hofer, Lucas. “M² Measurement.” DataRay Inc., 12 Apr. 2016, www.dataray.com/blog-m2-measurement.html.
Strehl, Karl W. A. “Theory of the telescope due to the diffraction of light,” Leipzig, 1894.
Mahajan, Virendra N. "Strehl ratio for primary aberrations in terms of their aberration variance." JOSA 73.6 (1983): 860-861.