레이저 공진기 모드

본 내용은 레이저 옵틱스 리소스 가이드의 단원 6.1에 해당합니다.

레이저 빔의 형태는 이득 매질(gain medium)에서 증폭되는 레이저 광선의 공진기 공동(resonator cavity)에 의해 결정됩니다. 레이저 공진기(laser resonator)는 일반적으로 빛의 출사를 막기 위해 내부 전반사를 활용하는 고반사형 유전체 미러 또는 모놀리식 크리스털을 사용해 형성됩니다(그림 1). 레이저 공진기는 기하학적 구조¹에 따라 일반적으로 아래와 같이 분류할 수 있습니다.

평면 평행 공진기: 레이저 파장 절반의 정수배와 동일한 거리로 분리된 두 개의 플랫 미러
공중심 공진기: 곡률 반경이 같고 곡률의 중심이 일치하는 두 개의 구면 미러
공초점 공진기: 곡률 반경이 갖고 초점이 일치하는 두 개의 구면 미러
링 공진기: 반사광의 total closed loop path가 레이저 파장 절반의 정수배와 동일한 두 개 이상의 반사체로 구성된 링

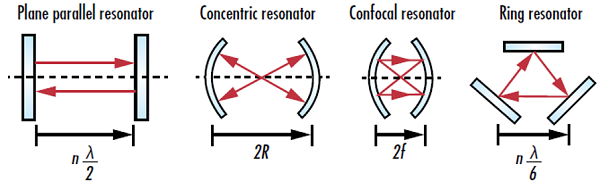
그림 1: 일반적인 유형의 네 가지 레이저 공진기 구조로서 n은 정수값, λ는 레이저 파장, R은 곡면 미러의 곡률 반경, f는 곡면 미러의 초점 길이를 가리킴

공진기 공동은 반사 횟수가 무한대에 가까워지는 경우에도 반사광이 공동 내에 머물러 있다면 "안정적" 상태를 보입니다(그림 2). 이와 같은 경우 빛이 공동을 빠져나갈 수 있는 유일한 방법은 부분 반사형 미러를 통과하는 것입니다. 반면에 반사 횟수가 무한대에 가까워지면서 반사광이 연속적으로 분산될 경우 공진기 공동은 "불안정" 상태로 간주합니다. 이렇게 되면 빔의 크기는 반사체보다 커질 때까지 증가하다가 결국 시스템을 빠져나가게 됩니다. 안정적인 공진기는 높은 gain을 달성하고 방향성을 향상시키기 위해 최대 출력이 2kW인 레이저에 자주 사용됩니다. 불안정 공진기는 반사체의 손상 가능성을 줄이기 위해 출력이 더 높은 레이저에 주로 사용됩니다.¹

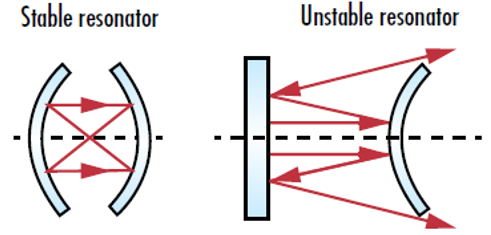
그림 2: 안정적인 레이저 공진기는 모든 반사광을 공동 영역 내에 가두며 반면 불안정한 공진기는 결국 반사광이 공동 영역을 빠져나갈 때까지 반사광을 확산시킴

공진기 공동의 경로 길이는 세로형 공진기 모드를 결정하거나 공동 내에서 정상파(standing wave)를 일으키는 전기장의 분포를 밝혀낼 때 사용됩니다. 이때 빔의 모드에 따라 빔의 형태가 결정됩니다. 이와 같은 모드는 진폭 프로파일을 유지하고 공진기 내에서 루프 경로 하나를 완전히 폐쇄시킨 후 자가 재생을 합니다(공진 내에서의 손실로 인해 약간의 파워 손실이 잠재적으로 발생하는 경우와는 별개임). 공진기 모드를 일으키기 위해서는 하나의 폐쇄 루프 경로에서 2π의 정수배와 동일한 위상 변이 또한 경험해야 합니다(그림 3).

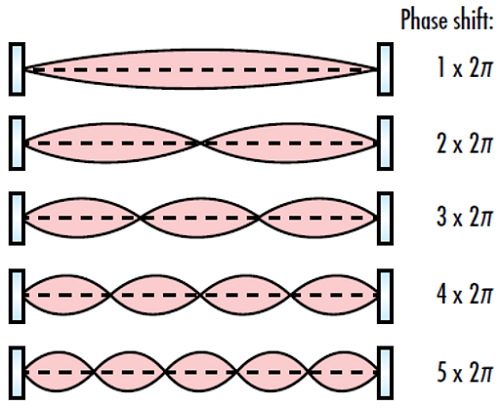
그림 3: 공진 모드를 일으키려면 광학 공진기에서 전체 루프의 위상 변이가 2π의 정수배가 되어야 함

레이저 공진기 모드의 가장 단순한 유형은 횡단 전자기 모드(TEM_nm)로도 알려진 에르미트-가우시안 모드(Hermite-Gaussian mode)로서 전기장 프로파일의 근사치는 가우시안 함수로부터 산출된 값과 에르미트 다항식²을 이용해 구할 수 있습니다.

$$ E_{nm} \! \left(x, y, z \right) = E_0 \frac{w_0}{w \! \left( z \right)} \, \cdot \, H_{n} \left( \sqrt{2} \frac{x}{w \! \left( z \right)} \right) \cdot \exp{\left( -\frac{x^2}{w \! \left( z \right) ^2} \right)} \, \cdot \, H_m \left( \sqrt{2} \frac{y}{w \! \left( z \right)} \right) \cdot \exp{\left( -\frac{y^2}{w \! \left( z \right) ^2} \right)} \, \cdot \, \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right)}{2 R \! \left( z \right) } \right] \Bigg]} $$

\begin{align} E_{nm} \! \left(x, y, z \right) = & \, E_0 \frac{w_0}{w \! \left( z \right)} \, \cdot \, H_{n} \left( \sqrt{2} \frac{x}{w \! \left( z \right)} \right) \\ & \cdot \exp{\left( -\frac{x^2}{w \! \left( z \right) ^2} \right)} \, \cdot \, H_m \left( \sqrt{2} \frac{y}{w \! \left( z \right)} \right) \cdot \exp{\left( -\frac{y^2}{w \! \left( z \right) ^2} \right)} \\ & \cdot \, \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right)}{2 R \! \left( z \right) } \right] \Bigg]} \end{align}

$$ E_{nm} \! \left(x, y, z \right) = E_0 \cdot H_n \cdot H_m \frac{w_0 \, x \, y}{\left[ w \! \left( z \right) \right]^3} \cdot \exp{\left[ - \left( \frac{x}{w \! \left( z \right)} \right)^2 \right]} \cdot \exp{\left[ - \left( \frac{y}{w \! \left( z \right)} \right)^2 \right]} \cdot \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right) }{2 R \! \left( z \right)} \right] \Bigg]} $$

\begin{align} E_{nm} \! \left(x, y, z \right) = & \, E_0 \cdot H_n \cdot H_m \frac{w_0 \, x \, y}{\left[ w \! \left( z \right) \right]^3} \cdot \exp{\left[ - \left( \frac{x}{w \! \left( z \right)} \right)^2 \right]} \cdot \exp{\left[ - \left( \frac{y}{w \! \left( z \right)} \right)^2 \right]} \\ & \cdot \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right) }{2 R \! \left( z \right)} \right] \Bigg]} \end{align}

E₀는 최대 시야
x와 y는 빔의 단면을 정의하는 축
z는 전파의 축
w₀는 빔의 웨이스트
w(z)는 주어진 z 값에서 빔의 반경
H_n(x)와 H_m(x)는 음수가 아닌 정수 지수 n과 m으로 이루어진 에르미트 다항식
k는 파상수(k=2π/λ)
z_R은 레일리 거리
R(z)는 웨이브프론트의 곡률 반경

정수 n과 m은 각각 x와 y 방향에서 빔의 형태를 규정합니다. 이상적인 가우시안 빔은 n과 m이 모두 0일 때 발생하는 TEM₀₀ 모드에서 정의됩니다(그림 4). 가우시안 빔에 관한 더 많은 정보는 당사 어플리케이션 노트 가우시안 빔의 전파 편에서 자세히 다룹니다. n과 m의 기타 모든 값은 더 복잡한 공진기 모드를 생성합니다.³ 그림 5에서는 n과 m의 값이 0에서부터 3일 때 차수가 가장 낮은 에르미트-가우시안 모드의 횡단면 형상을 확인할 수 있습니다.

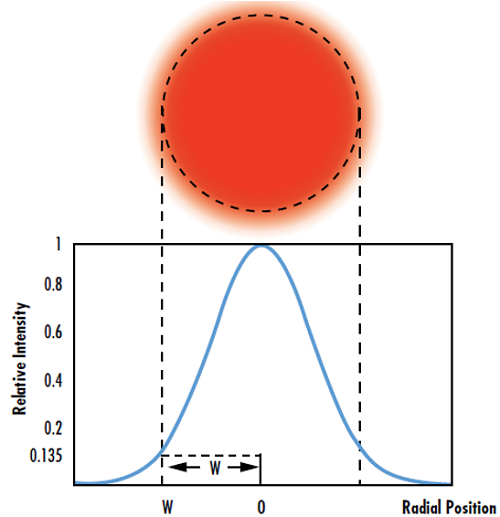
그림 4: 에르미트-가우시안 공진기 모드 TEM00는 완벽한 가우시안 빔과 일치

그림 4: 에르미트-가우시안 공진기 모드 TEM₀₀는 완벽한 가우시안 빔과 일치

그림 5: n과 m의 값이 0 - 3의 범위일 때 가장 낮은 차수의 에르미트-가우시안 공진기 모드의 단면

참고 문헌

“Section 2.6: Various Laser Resonators.” Advanced Manufacturing Laboratory, Columbia Engineering, www.aml.engineering.columbia.edu/ntm/level2/ch02/html/l2c02s06.html.
Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
Paschotta Rüdiger. Field Guide to Lasers. SPIE Press, 2008.

이전 단원 다음 단원