광학 제품 사용 사례
사용 사례 1: Detector Systems | 사용 사례 2: Selecting the Right Lens | 사용 사례 3: Building a Projection System
사용 사례 1: Detector Systems
모든 광학 시스템에는 어떤 형태로든 예비 설계가 필요합니다. 설계 시작이 가장 어려운 단계인 경우가 많지만 시스템의 주요 사양 여러 가지를 식별해 두면 초안 작성에 도움이 될 것입니다. 다음 질문은 간단한 detector 또는 emitter 시스템 설계 과정을 설명합니다.
목적: 빛이 향하는 곳은 어디일까요?
이미징 용도에 단순한 lenses를 사용하곤 하지만 많은 경우, 목적은 시스템의 한 점에서 다른 점으로 빛을 투사하는 것입니다. 거의 모든 emitters, detectors, lasers, 그리고 fiber optics에 이런 종류의 광선 조작을 위한 렌즈가 필요합니다. 설계할 시스템 유형을 결정하기 전에 먼저 대답해야 할 중요한 질문 하나가 바로 "빛이 향하는 곳은 어디일까요?"라는 질문입니다. 설계 목적이 가능한 한 aberrations 없이 모든 입사광을 detector에 채우는 것이라면 plano-convex (PCX) 또는 double-convex (DCX) lens와 같은 단순한 singlet lens를 사용할 수 있습니다.

그림 1: Detector 용도에서 FOV Limit로서의 PCX Lens
그림 1에서는 렌즈의 Diameter(D1) 및 Focal Length (f)를 포함한 몇 가지 중요한 사양과 함께 PCX lens를 보여 줍니다. 그림 1에서는 또한 Full Field of View (FFOV) 근사치 또는 정확한 공식에 의해 표시된 바와 같이 detector의 diameter에 따라 시스템의 Field of View (FOV)가 :
어떻게 제한되는지 설명합니다.
스캐닝 시스템에 사용되는 detectors에 있어 중요한 측정값은 스캔 중의 한 순간에 detector가 마주하게 되는 각도인 Instantaneous Field of View (IFOV)입니다.
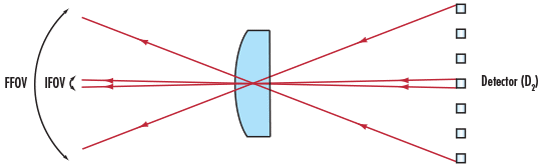
그림 2: Instantaneous FOV
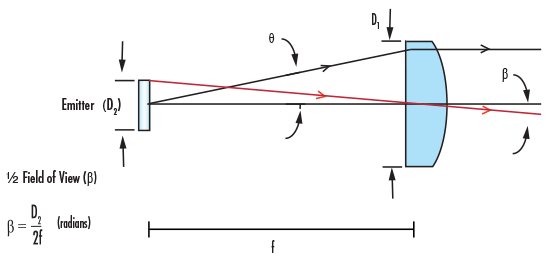
그림 3: Emitter 용도에서 FOV Limit로서의 PCX Lens
빛 투과율: 최초에 존재했던 빛의 양은 얼마입니까?
빛이 어디를 향할지 파악하는 것은 light-projecting system 설계의 첫 번째 단계에 지나지 않습니다. 물체 또는 소스로부터 얼마나 많은 양의 빛이 투과되는지 아는 것만큼 중요합니다. 투과 효율은 detector에 수신된 빛의 양을 통해 "최초에 존재했던 빛의 양은 얼마입니까?"라는 질문에 답하는 것을 바탕으로 합니다. 렌즈의 Numerical Aperture (NA) 및 F-number (f/#)는 f, D, index of refraction (n) 및 Acceptance Angle (θ)을 기준으로 렌즈가 모을 수 있는 빛의 양을 측정합니다. 그림 4에서는 f/# 및 NA 사이의 관계를 보여 줍니다.
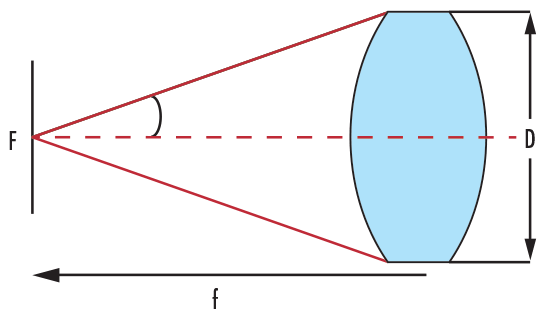
그림 4: f/# 및 NA가 표시된 DCX Lens
이 관계는 공식 1.5에 따라 수학적으로 표현할 수 있습니다. Diameter가 클 수록, f/#가 작아지고 시스템에 더 많은 빛이 들어옵니다. 가장 효율적인 시스템을 만들려면 광원으로부터의 emitted cone을 렌즈의 acceptance cone과 일치시키는 것이 가장 좋은데 이렇게 하면 렌즈 영역을 초과해 채우거나 다 채우지 못하는 상황을 피할 수 있습니다.
(1.4)$$ f/\# = \frac{f}{D} $$
Optical Throughput: 시스템을 통과하는 빛의 양은 얼마입니까?
emitter에서 detector로 빛을 전송하기 위한 도구로서 렌즈를 사용할 경우 전송된 빛 에너지의 정량적 측정치인 Throughput(TP)을 고려하는 것이 중요합니다. 다시 말해, "시스템을 통과하는 빛의 양은 얼마입니까?"라는 질문에 대한 답에 따라 사용할 렌즈의 형태와 시스템 구성이 결정됩니다. emitters 및 detectors는 빛의 면적이며 point sources가 아니기 때문에 Diameter와 Focal Length(f/#에 의해 지정됨) 간의 비율이 일정할 때에도 렌즈의 diameter는 TP에 영향을 줍니다.
그림 5는 공식 1.7에서 표시된 바와 같이 Throughput(TP)의 기본 개념을 보여 줍니다. 이 공식에서 A는 물체(광원)의 면적, Ω는 Solid Angle, 그리고 z는 Object Distance(이미지 공간에서 해당 켤레각은 A', Ω', 그리고 z'로 표시됨)입니다.
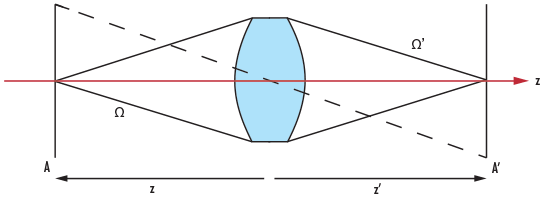
그림 5: Throughput이 표시된 DCX Lens
Solid angle은 Ω = A/r2로 정의되며 이 때, A는 렌즈 표면의 면적이고 반경(r)은 Ω 또는 Ω'에 대해 각각 렌즈부터 물체(z) 또는 image plane (z')까지의 거리입니다.
detector에 도달하는 빛의 양은 lens aperture limitations으로 인해 시스템 내에서 빛이 물리적으로 차단되는 vignetting으로 인해 감소될 수 있습니다. 하지만, 일부 시스템은 의도적으로 vignetting을 활용하는 경우도 있는데 이를 통해 이미지 품질에 부정적인 영향을 주는 stray light를 제거할 수 있습니다. 시스템을 올바로 배열하면 stray light와 의도하지 않은 vignetting을 줄일 수 있다는 점을 유념해야 합니다.
Aberrations: 이미지가 어떻게 보입니까?
시스템에 얼만큼의 빛이 통과하는지 파악하는 것이 중요하지만 시스템 내부에서의 aberrations도 중요한 역할을 합니다. "이미지가 어떻게 보입니까?"라는 질문에 대한 답은 시스템의 디자인을 개선해 aberrations을 줄이고 이미지 품질을 향상시킬 수 있습니다. Aberrations은 제작 또는 배열에 관계 없이 모든 광학 시스템 고유의 오류입니다. 모든 광학 시스템에는 aberrations이 포함되기 때문에 성능과 비용 사이의 균형을 조정하는 것은 어떤 디자이너에게든 중요한 결정 사항입니다. coma (aperture에 따른 배율 또는 이미지 크기 변화), spherical (paraxial focus 앞뒤로의 light rays focusing), 그리고 astigmatism (가로 및 세로축에 각각 하나의 focus point를 가짐)과 같은 몇 가지 기본적인 aberrations은 f/#를 늘리면 다음과 같은 관계를 통해 감소시킬 수 있습니다.
사용 사례: Detector System
예를 들어, 그림 3에서와 같이 ¼" diameter의 fiber optic light guide에서 빛이 방출되는 시스템을 고려해 보십시오.
- 최초 매개변수
NLight Guide의 NA = 0.55
광원(Emitter)의 Diameter = 6.35mm
공기의 Index of Refraction = 1 - 계산된 매개변수
F- Number (f/#)
f/1인 PCX lens는 f/#가 1임을 의미하며 최대한의 집광을 위해 light guide 앞에 배치하기에 적합합니다. 공식 1.4에 따라 f/#가 1이면 렌즈의 diameter와 focal length는 동일합니다. 다시 말해, diameter가 12mm인 렌즈일 경우 focal length도 12mm입니다.
Full Field of View (FFOV)
SSteradians는 3차원 공간에서의 2차원 각도에 해당되는데 이는 렌즈의 가장자리에서 가장자리까지의 각도가 2차원에 해당되기 때문입니다. emitter에서 렌즈까지의 간격이 짧거나 렌즈 diameter가 커질 수록 steradians 값이 커집니다. solid angle이 가질 수 있는 최대값은 4π, 또는 약 12.57이며 이는 모든 공간의 solid angle에 해당됩니다.
이 시스템의 Throughput (TP)을 계산하려면 먼저 Area of the Source (공식 1.11), Area of the Lens (공식 1.12), 그리고 Solid Angle (공식 1.13)을 계산해야 합니다. 다양한 소스(이 예에서는 light guide)의 빛을 집광하는 데 있어서 일반 원리로서 소스로부터 1 focal length 거리에 렌즈를 배치하십시오.
시스템이 n이 1에 수렴하는 free space에 있을 때 n2는 최종 계산에 반영되지 않습니다.
사용 사례 2: 올바른 렌즈 선택
이미지 품질이 높다는 것은 aberrations이 적다는 것과 비슷합니다. 결과적으로 디자이너들은 단일 렌즈 솔루션에 비해 더 높은 이미지 품질을 얻기 위해 두 개 이상의 렌즈를 사용하곤 합니다. 용도에 따라 소스 유형, 공간적 제약, 비용 등 여러 가지 요소들이 올바른 렌즈 선택에 반영됩니다.
그림 6a - 6e는 relay lens 또는 1:1 이미징 용도로 다양한 렌즈 시스템을 비교합니다. 이 사례에서 다음과 같은 일련의 비교를 통해 요약된 내용을 통해 선택한 렌즈의 형태와 광학 특성에 따라 이미지 품질이 어떤 영향을 받는지 쉽게 볼 수 있습니다.
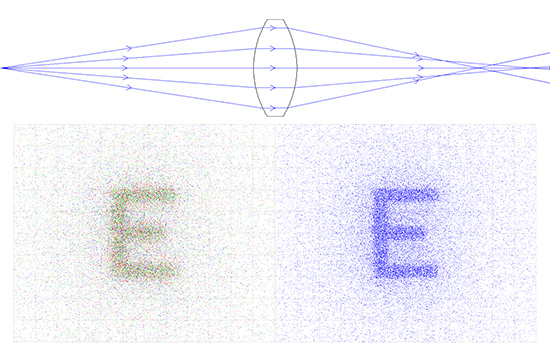
그림 6a: DCX Lens Relay System: 25mm EFL x 20mm Entrance Pupil Diameter (왼쪽은 컬러, 오른쪽은 흑백)
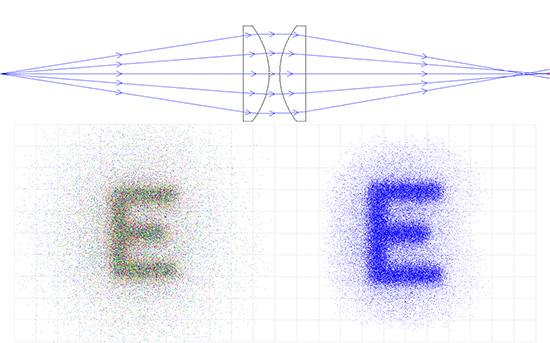
그림 6b: PCX Lens Relay System: 50mm EFL x 20mm Entrance Pupil Diameter (왼쪽은 컬러, 오른쪽은 흑백)
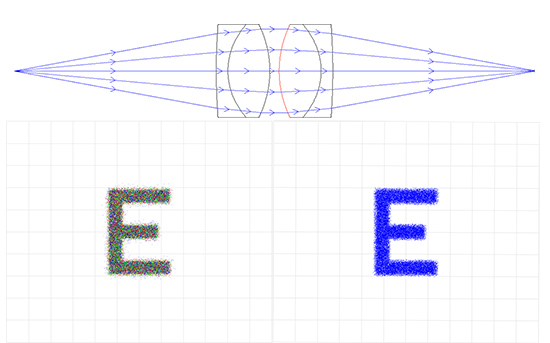
그림 6c: Achromatic Lens Relay System: 50mm EFL x 20mm Entrance Pupil Diameter (왼쪽은 컬러, 오른쪽은 흑백)
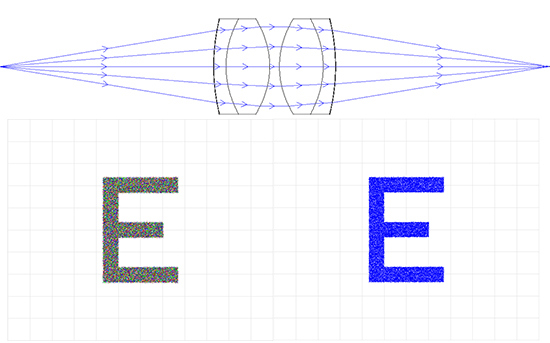
그림 6d: Aspherized Achromatic Lens Relay System: 50mm EFL x 50mm Entrance Pupil Diameter (왼쪽은 컬러, 오른쪽은 흑백)
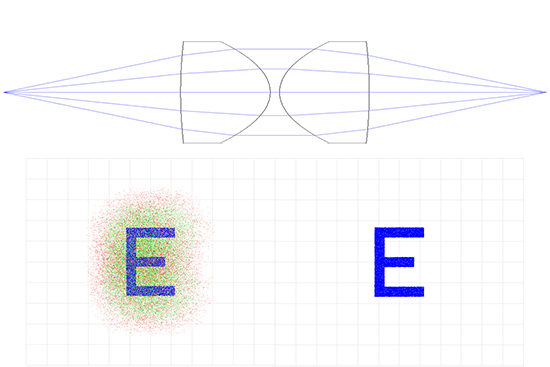
그림 6e: Aspheric Lens Relay System: 50mm EFL x 40mm Entrance Pupil Diameter (왼쪽은 컬러, 오른쪽은 흑백)
사용 사례: Single Element Lens System
double-convex (DCX) lens는 대칭 형태를 갖고 있어 plano-convex (PCX) lens와 같이 한쪽이 다른 쪽보다 빛을 더 많이 휘게 하지 않고 렌즈의 양쪽이 동일한 능력을 가져 1:1 이미징용으로 최적의 single element 렌즈로 간주됩니다. 렌즈 시스템이 단 한 개의 렌즈로 구성되어 있기 때문에 aperture stop이 본질적으로 렌즈이어서 많은 aberrations의 감소가 가능합니다. 이런 이류로 DCX lens는 1:1 이미징을 위한 single PCX lens에 적합합니다. 하지만, 낮은 f/#에서는 여전히 상당한 spherical aberration 및 coma가 발생한다는 점을 유념해야 합니다. 이 aberration들은 single lens의 Shape Factor (S)에 의해 발생합니다.
여기에서 R1 및 R2는 각 렌즈 표면의 반경입니다.
object 또는 소스는 infinity인 상태에서 렌즈 한 개만 필요한 경우 시스템에 유해한 aberration을 줄이기 위해 보다 나은 shape factor를 찾을 수 있습니다. 예를 들어, spherical aberration을 줄이기 위해 다음 공식을 사용해 이상적인 shape factor를 계산할 수 있습니다.
이 때, n은 Glass Substrate의 Index of Refraction, p는 Position Factor, z는 Object Distance(음수 값으로 측정됨), 그리고 z'는 Image Distance(양수 값으로 측정됨)입니다.
infinity의 object의 coma를 줄이려면 다음 공식으로 Shape Factor를 계산할 수 있습니다.
object가 infinity에 있는 상태에서 1.5 (N-BK7가 1.517)의 index를 갖는 glass의 경우, 약 0.8의 Shape Factor를 사용하면 coma 및 spherical aberrations 모두의 보정 균형이 조절됩니다.
사용 사례: Double Element Lens System
시스템 성능 향상을 위해 DCX의 두 배에 해당되는 focal length를 갖고 있고 aperture stop이 센터에 있는 두 개의 동일한 PCX lenses로 단일 DCX lens를 교체할 수 있습니다. 이렇게 하면 focal length는 출력에 반비례하므로 각 렌즈 표면의 출력이 분할됩니다. 각 렌즈의 출력이 저하됨에 따라 시스템의 spherical aberration 발생이 감소합니다. 두 개의 렌즈를 사용함으로써 각 표면의 출력이 합해져 전체 focal length는 동일하면서도 spherical aberration은 감소합니다. diameter 역시 동일하게 유지되며 f/#는 단일 DCX 렌즈를 사용하든 두 개의 PCX 렌즈를 사용하든 변화가 없지만 spherical aberration은 f/#가 큰 경우에도 감소합니다.
볼록면은 볼록면 사이에 있는 aperture stop에 거의 닿을 정도로 가까워집니다. 볼록면을 가장 긴 conjugate distance쪽으로 향하게 함으로써 보다 나은 이미지 품질이 확보됩니다..
사용 사례: Achromatic Lens System
또 다른 옵션은 두 개의 achromatic lenses 또는 achromats을 사용하는 것입니다. achromatic lens는 positive low-index (crown) element 및 negative high-index (flint) element가 결합된 두 개의 광학 부품으로 구성됩니다. achromats을 사용하면 polychromatic (white light, 복수 파장) imaging이 향상될 뿐 아니라 spherical aberration 및 coma도 감소합니다. 두 개의 렌즈가 모두 볼록면이 서로를 향하는 achromats이라면 단일 렌즈(DCX 또는 2개의 PCX)를 사용하는 동일한 시스템에 비해 aberrations이 크게 감소해 훨씬 우수한 이미징 시스템을 구성할 수 있습니다. apertures 또는 f/#가 클 경우 spherical aberration은 무시할 수 있을 정도지만 chromatic aberration은 achromats을 사용하면 크게 감소합니다. 시판 중인 많은 relay lens 시스템이 이런 유형의 four element 구성을 이용합니다.
singlet lenses에 비해 achromatic lenses를 사용할 경우의 장점에 대한 자세한 내용을 보려면 Achromatic Lens를 사용하는 이유는 무엇일까요?를 참조하십시오..
사용 사례: Aspheric Lens System
구의 일부를 사용해 만들어지는 PCX, DCX 및 achromatic lenses와 달리, aspheric lens는 sphere 또는 cylinder와 다른 곡률을 갖는 렌즈로서 hyperbola 또는 parabola의 일부를 사용해 제작됩니다. aspheric lenses 또는 aspheres의 핵심 개념은 radius of curvature가 렌즈의 optical axis로부터 방사상으로 달라진다는 것입니다. 결과적으로 aspheric lenses는 spherical aberration을 쉽게 보정하며 off-axis aberrations 보정에 안성맞춤입니다.
Aspheric lenses는 많은 시스템에서 사용됩니다. 하나의 aspheric lens가 둘 이상의 spherical lenses를 대체할 수 있어 시스템 공간과 비용을 줄여 줍니다. aspheric lenses의 생산, 설계 및 사용에 대한 자세한 내용은 Aspheric Lenses의 모든 것을 참조하십시오.
| 렌즈 시스템 유형 | Spherical Aberration | Chromatic Aberration |
|---|---|---|
| DCX Singlet | 높음 | 높음 |
| 2 PCX | 중간 | 높음 |
| 2 Achromats | 낮음 | 아주 작음 |
| 2 Aspherized Achromats | 아주 작음 | 아주 작음 |
사용 사례 3: PROJECTION SYSTEM 구축
맞춤형 projector system 설계에는 시간이 많이 들고 비싼 경우가 많습니다. 그럼에도 불구하고 쉽고 비용 대비 효과적인 프로세스를 위해 따라야 할 몇 가지 간단한 절차가 있습니다. 여러 가지 시스템 설계 용도에 다음과 같은 기본 절차를 적용할 수 있습니다.
맞춤형 설계 절차:
- 시스템을 여러 부분으로 분리 – 광학 용도는 간단한 magnifiers부터 laser beam conditioning에 이르기까지 종류가 많고 다양합니다. 하지만 대부분의 용도는 거의 개별적으로 개발할 수 있는 소형 모듈들로 나눌 수 있습니다.
- 각 부분을 별도 설계 – 각 모듈을 분리해 개별 성능이 최적화되도록 설계함으로써 시스템 전체 성능에 도움을 줄 수 있습니다. 이 점은 한 모듈의 최적화가 다른 모듈의 설계에 부정적인 영향만 주지 않는 한 사실이며 서로 다른 부분들을 설계할 때 전체 시스템을 생각하는 것이 중요합니다.
- 컴퓨터를 사용한 최적화 – 최초 규격을 계산한 뒤 해당 디자인을 ZEMAX 또는 Code V와 같은 렌즈 디자인 소프트웨어에 입력하는 것이 전체 디자인뿐 아니라 각각의 모듈까지 최적화하는 최상의 방법입니다. 각 시스템 모듈을 최적화하면 적절한 mounting components를 선택하기 위한 모범 사례 시나리오를 얻을 수 있습니다. 또한 계산을 통해 합리적인 데이터가 산출되도록 보장하기 위한 확인 작업 역할도 합니다.
- 시스템 조립 – 각 모듈을 설계한 뒤 전체 시스템을 조립해야 합니다. 모듈을 결합하기 전에 각각의 모듈을 점검해 올바로 작동하는지 확인한 뒤에 시스템에 결합해야 합니다. 시스템을 조립한 후 렌즈 디자인 소프트웨어를 통한 시험과 전체 시스템 작동을 통해 시스템 내부에서 모듈들이 함께 올바로 작동하는지 확인해야 합니다.
- 부품 선택 – 대부분의 렌즈 디자인 소프트웨어 패키지에는 기성품 렌즈 처방 라이브러리와 "closest-match" 알고리즘이 포함되어 있어 맞춤형 부품 대신 실제 렌즈와 품목을 선택하는 데 도움을 줍니다. 렌즈 디자인 소프트웨어는 존재하지 않는 glass number에 최적화할 수도 있지만 closest-match는 구매할 수 있는 아주 유사한 glass 유형을 알려 줍니다. 올바른 glass를 선택하는 것을 넘어 시스템에 적합한 기기를 찾는 것이 중요합니다. lens holders 및 system mounting을 선택하기 전에 크기, 무게, 그리고 외형을 고려해야 합니다.
glass 선택에 대한 보다 자세한 내용을 보려면 Optical Glass를 참조하십시오.
구형 slide projector와 같은 대부분의 projectors에는 2개의 핵심 모듈인 condenser lens system 및 projector lens system이 들어 있습니다. condenser lens system은 슬라이드를 고르게 밝혀 주며 projector lens system은 슬라이드의 이미지를 스크린에 투사합니다. 간단한 부품과 방법을 이용해 각각의 모듈을 만들 수 있습니다. 이 예에서는 큰 aperture와 아주 다양한 focal lengths를 이용할 수 있는 25mm diameter optics를 사용합니다.
부품 1: Projection Lens System
부품 1: Projection Lens System projection lens system은 reticle image의 투사 거리 및 원하는 배율에 의해 제한됩니다. 대부분의 projection systems은 white light를 사용하므로 achromatic lenses를 사용할 때 최상의 이미지를 얻을 수 있습니다. 사용할 achromat을 결정하려면 투사된 이미지와 projection lens system 사이의 거리 (I), 그리고 원하는 배율 (M)을 결정해야 합니다. 배율은 렌즈의 focal length를 이용하거나 (공식 3.1) 이미지에서 object까지의 거리를 이용해 (공식 3.2) 계산할 수 있습니다.
부품 2: Condenser Lens System
condenser lens system은 다양한 광원으로부터 빛을 모아 굴절시킨 뒤 집광해 projector lens system에 비춥니다. 전통적인 condenser lens system은 그림 7에서와 같이 볼록면이 상호 마주 보게 장착된 2개의 PCX lenses로 구성됩니다. 첫 번째 렌즈는 illuminator(object 또는 projector)로부터 divergent light cone을 모으고 두 번째 렌즈는 convergent cone (이미지)으로 빛을 출력해 reticle을 조명합니다.

그림 7: 기본적인 Projection System
암묵적으로, projection lens 솔루션은 condenser lens system의 일부를 정의하며 이것이 바로 projection lens system을 먼저 설계하는 것이 중요한 이유입니다. condenser lens system부터 projector lens system까지의 거리는 reticle부터 projector lens system까지의 거리 이상입니다.
사용 사례: Projection System 설계
- 최초 매개변수
렌즈 Diameter = 25mm
이미지 거리 = 투사 거리 = 250mm
배율 = 2.5X - *계산된 매개변수
Object Distance 또는 Reticle까지 거리
projection lens system 제작에는 25mm diameter의 100mm focal length achromatic lens 2개가 적합합니다. 25mm diameter lenses는 큰 apertures와 기계 부품과의 호환성, 그리고 다양한 coatings 및 focal length로 인해 사용하기 아주 좋습니다.
PCX Condenser Lens의 Focal Length
projection system을 완성하려면 25mm diameter의 250mm focal length PCX lenses 2개가 필요합니다.































































혹은 지사별 연락처 확인
견적 도구
재고번호 입력 후 바로 시작
Copyright 2023, 에드몬드 옵틱스 코리아 사업자 등록번호: 110-81-74657 | 대표이사: 앙텍하우 | 통신판매업 신고번호: 제 2022-서울마포-0965호, 서울특별시 마포구 월드컵북로 21, 7층 (서교동 풍성빌딩)